EXAFS spectroscopy: a powerful tool for the study of local vibrational dynamics
Abstract
Extended X-ray absorption fine structure (EXAFS) spectroscopy is an ideal technique for studying the local vibrational dynamics of materials due to its sensitivity to short-range order, correlation of atomic motion and anharmonicity. However, despite this, EXAFS is widely employed to investigate the local structure but its use in the study of local dynamics is far more limited. In this brief review, the potential of EXAFS as a vibrational probe is presented with the aim of promoting its application in the study of the local dynamics of solid-state materials.
Keywords
INTRODUCTION
Knowledge of vibrational dynamics is fundamental for understanding the physical properties of materials. Various experimental and theoretical approaches are used to study vibrational dynamics in materials, ranging from Bragg diffraction to vibrational spectroscopy[1-6], or from ab initio calculations to molecular dynamics[7-9]. From an experimental perspective, X-ray and neutron diffraction can give precise parameters that describe the dynamic (but also static) displacements of atoms in crystals, such as mean-square atomic displacements[10, 11]. Inelastic neutron and X-ray scattering can be used to measure phonon dispersion curves
Alternatively, extended X-ray absorption fine structure (EXAFS) spectroscopy[18] provides both unique and complementary information compared to that obtained from the techniques described above. In fact, in addition to being sensitive to short-range order and atomic sites, EXAFS is particularly sensitive to the correlation of vibrational motion, both parallel and perpendicular to the bond direction, and anharmonicity[19-22]. However, although these properties make EXAFS unique, it is largely employed as a structural probe rather than as a dynamic one.
In this brief review, the capabilities of EXAFS spectroscopy for the study of local dynamics are reported. The intention is to present, for non-specialists, an introduction to the use of EXAFS in studying the vibrational dynamics of materials. For readers who wish to deepen their knowledge of EXAFS, other more exhaustive references are available[23-25].
The review is organized as follows. Section 2 to control sequence contains a synthetic introduction to the theory of EXAFS and the cumulants method. Section 3 shows a comparison between EXAFS spectroscopy and Bragg diffraction. The relations connecting EXAFS parameters to atomic thermal displacements and the sensitivity of EXAFS to atomic correlation are also presented here. Section 4 shows the phenomenological relationship of EXAFS to anharmonicity, emphasizing the differences between the one-dimensional potential probed by EXAFS and the three-dimensional crystal potential. Section 5 provides some recommendations regarding the data analysis procedure to obtain more reliable results. Section 6 provides some examples of studies that show the potential of EXAFS in the study of local dynamics. Section 7 presents the conclusions of this review.
FUNDAMENTALS OF EXAFS
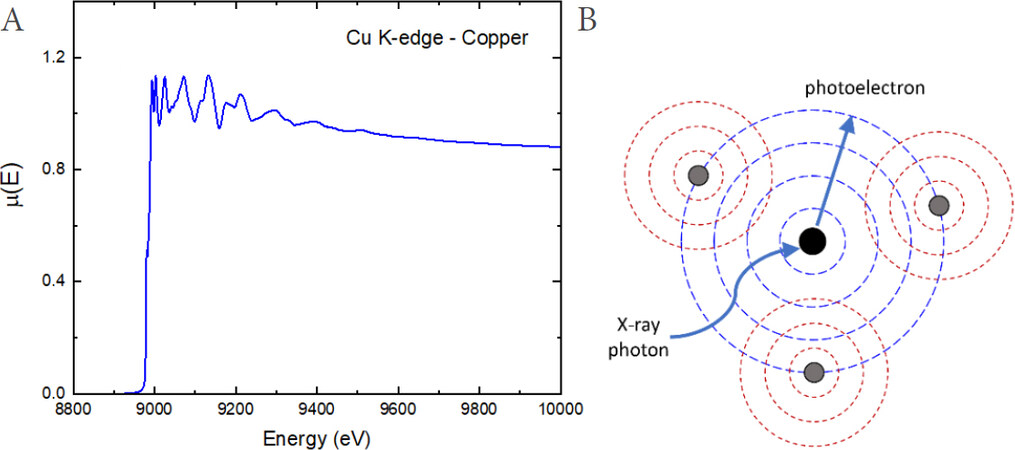
The aim of an EXAFS experiment is to measure the X-ray absorption coefficient of a selected atomic species as a function of energy [Figure 1A]. After the absorption edge, the absorption coefficient
Figure 1. (A) X-ray absorption coefficient (measured at the Cu K-edge of metallic copper at room temperature) plotted as a function of the incident beam energy. (B) Schematic view of EXAFS mechanism.
The EXAFS signal is defined as:
where
Figure 2. k
The starting point of EXAFS theory[24, 25, 28] is Fermi's golden rule within the dipole approximation, according to which the absorption coefficient can be written as:
where
where
However, thermal and structural disorder, including anharmonicity, can be better considered by removing the Gaussian approximation and by introducing a general one-dimensional distribution of distances between the absorbing and scattering atoms,
Note that, due to the spherical-wave nature of the EXAFS photoelectron and its limited mean free path
The integral in Equation (5) represents the structural part of the EXAFS formula and its logarithm can be developed in a Maclaurin series to obtain the final EXAFS formula, which is particularly suitable for the study of dynamics[25, 29, 30]:
where the parameters
As stated above, the EXAFS cumulants
while the higher order cumulants,
The exact relationships between
EXAFS VS. DIFFRACTION FOR ASSESSING LOCAL DYNAMICS
EXAFS spectroscopy and X-ray (or neutron) diffraction are complementary techniques.
● Owing to the limited mean free path of the EXAFS photoelectron, EXAFS is sensitive to short-range order, typically up to
● Because the mean lifetime of the EXAFS photoelectron (
● Finally, EXAFS measures the relative atomic vibrations, including the correlation of atomic motion, while diffraction only measures uncorrelated atomic vibrations from the atomic thermal factors included in the Rietveld analysis.
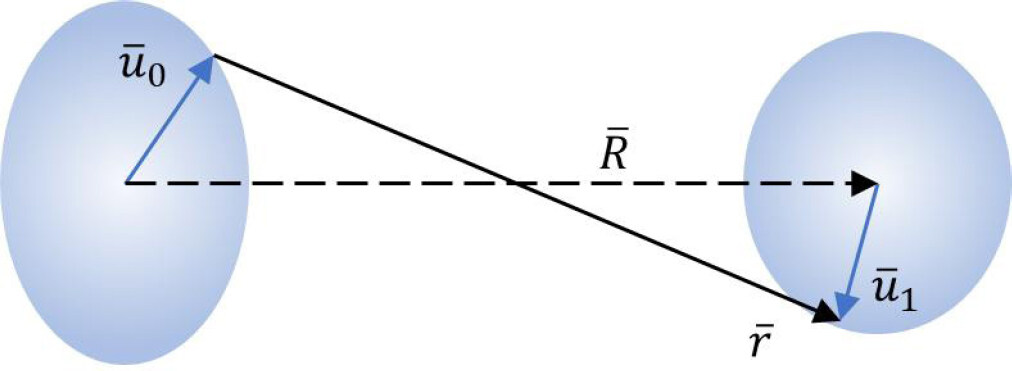
Let us now consider a pair of atoms, where the absorber atom of EXAFS and one of its neighbors are labeled as 0 and 1, respectively. Let
Figure 3. Instantaneous atomic displacements
and considering the projections of the relative displacement
the scalar distance
and thus its average value results in:
For harmonic displacements
The final term in Equation (14) is proportional to the atomic mean square relative displacement (MSRD) perpendicular to the bond direction,
The second cumulant of EXAFS,
which can be developed as:
The first two terms on the right-hand side of Equation (16) are the atomic mean square displacements (MSDs) of the absorber and backscatterer atoms along the bond direction, respectively, which can be obtained from Bragg diffraction. The third and final term in Equation (16) is known as the displacement correlation function (DCF) and is a measure of the degree of correlation of vibrational motion along the bond direction. As a result, the stronger the in-phase vibrational motion, the smaller the parallel MSRD
Finally, once the parallel and perpendicular MSRDs are known, we can determine the anisotropy of the relative thermal vibrations through the ratio:
which depends on the particular dynamic properties of the system. In the case of parallel-perpendicular isotropy,
In summary, EXAFS provides unique information on the local vibrational dynamics. This is because EXAFS measures the true bond distance, including the correlation of the atomic thermal vibrations, while Bragg diffraction measures the apparent bond distance, where the correlation is not included. The relationship between EXAFS and diffraction distances, given by Equation (14), allows us to determine the perpendicular MSRD of a given pair of atoms. The second cumulant of EXAFS, instead, allows us to determine the parallel MSRD by Equation (15) and, ultimately, the anisotropy of the relative thermal vibrations. The practical procedure for obtaining this information is presented in Section 5.
ANHARMONICITY
The distribution
where k
where, indicating with
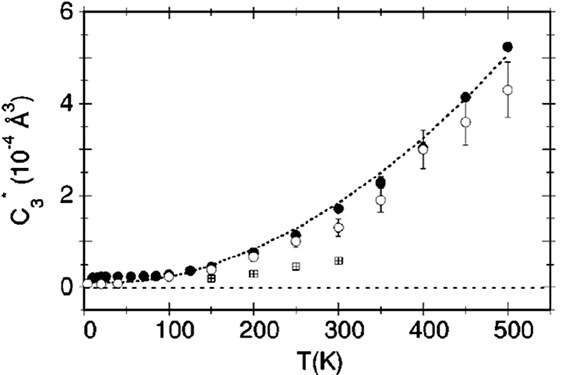
Note that, to the first order and in the classical approximation, the first and second cumulants grow linearly with temperature [Equations (19) and (20)], while the third and fourth cumulants grow, respectively, with the square and cube of the temperature [Equations (21) and (22)]. As an example, Figure 4 shows the first four cumulants of the first Se-Cd coordination shell of CdSe measured by EXAFS and calculated by classic molecular dynamics simulations[42, 43]. Analogous results were found in other compounds, such as copper or gold [Figure 5][36, 44]. Equation (20) also shows the second-order anharmonic correction to
Figure 4. First four cumulants of the first Se-Cd coordination shell of CdSe measured by EXAFS (solid circles) and calculated by classic molecular dynamics simulations (open circles)[43]. The dashed lines show the linear behavior for the first and second cumulants, in the classical limit, and the quadratic and cubic behavior for the third and fourth cumulants, respectively. © IOP Publishing. Reproduced with permission. All rights reserved.
Figure 5. Third (upper panel) and fourth (lower panel) cumulants measured by EXAFS for the first Cu-Cu coordination shell of copper. The continuous lines are the best fitting theoretical model with
However, in the treatment presented above, the effective pair potential
Therefore, even in a harmonic crystal, the one-dimensional real distribution
and the position of the maximum distribution thus obtaining:
Equations (26) and (27) correspond to Equations (14) and (15), respectively, because in the case of isotropy,
to include the shift with temperature of the effective pair potential. The bond thermal expansion
Figure 6. Comparison between bond thermal expansions
remains not entirely clear. Indeed, if the shift of the effective pair potential
Finally, as a last observation, according to Equation (28), the transverse vibrations also produce an intrinsic asymmetry (here with
DATA ANALYSIS STRATEGY
The aim of this section is to provide information regarding the data analysis procedure to obtain accurate EXAFS results for studying the local dynamics. It is assumed that the reader has knowledge of the standard EXAFS analysis procedure.
Equation (7) is employed to best fit the EXAFS signal and to determine the cumulants vs. temperature of a given coordination shell. In this equation, the scattering-path amplitude and phase shift,
The latter two terms have to be handled with careful attention. Indeed,
Firstly, all the experimental spectra have to be aligned in energy before the extraction of the EXAFS signals. This can be achieved through the reference spectra collected during the experiment, or, in the absence of these, through the spectrum at the lowest temperature, which can be used as reference. Obviously, in this second case, we must ensure that there is no shift in the edge position due to valence changes with temperature[27]. The error in the spectral alignment should not exceed 0.1 eV. The EXAFS signals can now be extracted by taking care to adopt the same process for all spectra.
Secondly, since there is no reason that
Figure 7. EXAFS best-fit results obtained for the first Sc-F shell of scandium fluoride[65]. Panels A and B show, respectively, the temperature behavior of
Thirdly, EXAFS cumulants higher than the second order must be considered in the analysis when possible. Indeed, the third and fourth cumulants have to be used to include anharmonicity and to thus obtain accurate values of the first and second cumulants, respectively[44, 46, 58]. This is particularly true for the interatomic distance expansion (
Figure 8. Bond thermal expansion
Finally, once the relative values
where
Equation (32) describes the thermal motion including the zero-point energy at 0 K and it can be used as the starting point to derive phenomenological models to account for the temperature dependence of the parallel MSRD. The first one is the correlated Debye model where only acoustic branches with linear dispersion are considered and the Brillouin zone is substituted by a Debye sphere[63, 64]. An alternative model that is easier to use is the correlated Einstein model, which considers three-dimensional quantum harmonic oscillators with the same frequency
where
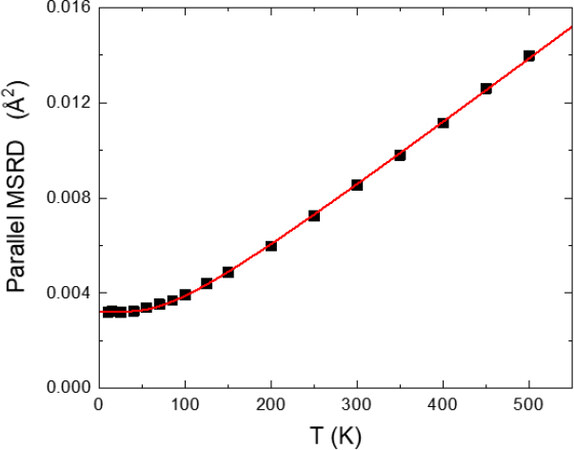
The Einstein model Equation (33) can be utilized to recover the absolute values of the parallel MSRD, i.e.,
Figure 9. Temperature dependence of
Similarly, the Einstein model can also be used to determine the absolute values of the perpendicular MSRD by fitting the temperature dependence of
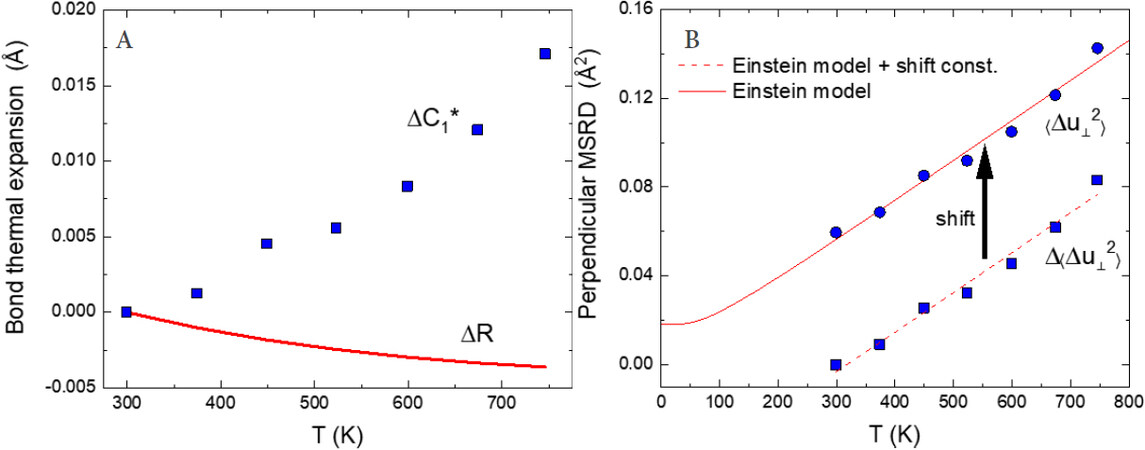
Figure 10A shows an example comparison between the true bond expansion
Figure 10. (A) Comparison between true bond expansion
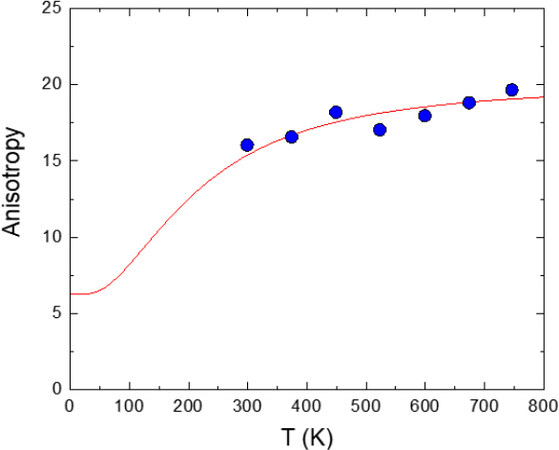
Figure 11. Resulting anisotropy of the relative thermal vibrations,
Although the correlated Einstein model is only a simple phenomenological model, it has the ability to reproduce satisfactorily the temperature behavior of
Figure 12. Parallel MSRD measured by EXAFS for the first Cu-Cu shell of copper (squares) and corresponding best-fit Einstein model (solid line)[36]. Despite its simplicity, the Einstein model satisfactorily reproduces the temperature behavior of MSRDs.
APPLICATIONS
In this section, examples of studies are provided that show the capability of EXAFS in the study of local dynamics. Obviously, good quality EXAFS data are required to obtain reliable information on the local vibrational dynamics. This is particularly true for the perpendicular MSRD, which is far more complicated to obtain than the parallel MSRD.
EXAFS as a benchmark for theoretical calculations
It is obvious that the local dynamics information obtained by EXAFS represents an excellent benchmark for theoretical calculations, because the EXAFS MSRDs depend not only on the frequency of the vibrational modes, but also on their eigenvectors. This is in addition to the EXAFS cumulants depending on the effective pair potential that is related to the real three-dimensional crystal potential. For example, EXAFS was recently used by Kuzmin and co-workers[68-70] to test the accuracy of several force-field models employed in molecular dynamics simulations. Force-field models that give lattice parameters, bulk moduli and elastic constants in good agreement with experimental data can still fail to reproduce the temperature dependence of EXAFS data. Thus, EXAFS provides additional information that enables discrimination between different models.
Various theoretical calculations have been carried out to predict EXAFS parameters and to validate interatomic potential models. The temperature dependence of the EXAFS cumulants up to the third or fourth order was calculated by Yokoyama et al.[71] for a Br
Figure 13. Third EXAFS cumulant for the first shell of fcc copper: from EXAFS data (full circles) and from path-integral Monte Carlo calculations with a many-body potential (open circles) and a two-body potential (crossed squares). The dashed line is the best-fitting model of experimental data. Figure taken from Ref.[72]. © APS Publishing. Reproduced with permission. All rights reserved.
Various theoretical calculations have been carried out to predict EXAFS parameters and to validate interatomic potential models. The temperature dependence of the EXAFS cumulants up to the third or fourth order was calculated by Yokoyama et al.[71] for a Br
Nanoparticles
Detailed EXAFS studies have been conducted to explore the local dynamics of nanoparticle systems. In one of the earliest studies, Rockenberger et al.[88] investigated the size dependence of the structural and dynamic properties of CdS nanoparticles in a size range from 1.3 to 12 nm. They observed that these properties are related to the surface-to-volume ratio and to the method of surface stabilization of the nanoparticles. A temperature-independent static contribution to the MSRD of the Cd-S bonds was identified. This static contribution is strongly size dependent. In contrast, the vibrational amplitudes of the Cd-S bonds are slightly reduced with decreasing particle size. The asymmetry of the interatomic Cd-S pair distribution, evaluated through the third EXAFS cumulant, is increased with reducing particle size and shows the possibility of distinguishing the crystal structure of CdS nanoparticles.
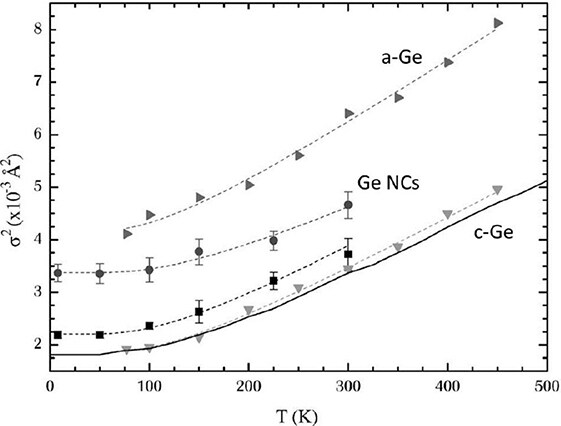
A decade later, EXAFS was used by Araujo et al.[89] to study the vibrational properties of Ge nanocrystals (NCs). The EXAFS Debye-Waller factor revealed that the Ge-Ge bonds of Ge NCs are stiffer than both bulk crystalline and amorphous Ge, with a static contribution that lies between theirs [Figure 14]. The higher static disorder in Ge NCs with respect to the crystal was attributed to the presence of undercoordinated atoms on the surface and the resulting internal strain. Moreover, the bond thermal expansion obtained for Ge NCs is smaller than for crystalline Ge, in good agreement with existing data for other nanocrystalline semiconductors[90, 91]. Somewhat different behavior was observed by Sprouster et al.[92], who investigated the size-dependent vibrational properties of Co nanoparticles by temperature-dependent EXAFS. Compared to bulk Co, the authors noted a softening of the Co-Co bonds in the smallest nanoparticles, attributed to the strong influence of undercoordinated bonds, as well as reductions in the average bond length and coordination number. Enhanced structural disorder and asymmetrical deviation from a Gaussian-like interatomic distance distribution with decreasing particle size were confirmed.
Figure 14. EXAFS Debye-Waller factor measured as a function of temperature in Ge nanocrystals (circles), bulk crystalline Ge (squares and down-triangles) and amorphous Ge (right-triangles), with the respective correlated Einstein model fits (dashed lines). The solid line is the Ge-Ge dynamic contribution in c-Ge from ab initio calculations[93]. The reduced slope of Debye-Waller for Ge NCs means that the Ge-Ge bonds in Ge NCs are stiffer than crystalline and amorphous Ge. Moreover, Ge-Ge static disorder is observed in Ge NCs, lying between that of c-Ge and a-Ge. Figure taken from Ref.[89]. © APS Publishing. Reproduced with permission. All rights reserved.
Furthermore, the vibrational properties of gold nanoparticles have also been subject to EXAFS studies. Comaschi et al.[94] studied the thermal behavior of Au nanoparticles with sizes ranging from 2.4 to 5.0 nm. With respect to the bulk crystal counterpart, the authors observed for the first four shells a progressive reduction of the average bond length and coordination number with decreasing particle size, as well as a simultaneous increase in the static disorder. More interestingly, a reduction of the Au-Au bond thermal expansion was found, with a curious crossover from an initial thermal expansion to a thermal contraction in the smallest particles, tentatively interpreted as being due to the presence of discrete electronic energy levels induced by the finite size particles[95]. Duan et al.[96] confirmed the contraction of the average Au-Au bond length, the decrease of coordination number and the presence of static disorder in Au147 nanoparticles compared to the bulk material. However, they were able to observe a bond expansion for the surface-surface bonds, accompanied by a softening of the vibrational modes, while the surface-core and core-core bonds contracted. A recent review by Timoshenko et al.[97] reports the latest advancements in the study of the structure and dynamics of metal nanoparticles by combining EXAFS spectroscopy and atomistic simulations.
A noteworthy EXAFS study of the local dynamics of nanoparticles was carried out by Hu et al.[98] for scandium fluoride. Static disorder and a decrease in the average bond length were observed for both the Sc-F and Sc-Sc distances with respect to the bulk counterpart. However, the most important result to be noted was the large stiffening of the average Sc-F bond bending, which resulted in a reduction of the Sc-F anisotropy and negative thermal expansion (NTE). The use of EXAFS spectroscopy to investigate NTE materials represents one of the most successful fields of EXAFS applications for studying vibrational dynamics, as described in the next section.
Negative thermal expansion materials
Thermal expansion represents a problem for many materials and engineering applications and its control is a challenge for materials design. After the discovery of materials that exhibit strong NTE over wide temperature ranges[99, 100], the interest in NTE has rapidly expanded and the prospect of controlling thermal expansion has become possible. Although it is known that NTE arises from a range of different mechanisms[101], the general comprehension of NTE (and related phenomena) is still incomplete. In this regard, EXAFS spectroscopy is of great help since it provides unique information on the local vibrational dynamics. Like EXAFS, the neutron pair distribution function (PDF) is sensitive to the atom-atom correlation, but the overlap of neighboring peaks in PDF analysis makes it extremely difficult to investigate the local dynamics of nearest neighboring bonds with sufficient accuracy.
To the best of our knowledge, the first EXAFS studies to investigate the local dynamics of NTE materials were performed on zirconium tungstate[102, 103], the most popular NTE material, and cuprite structures[35, 104, 105]. For ZrW
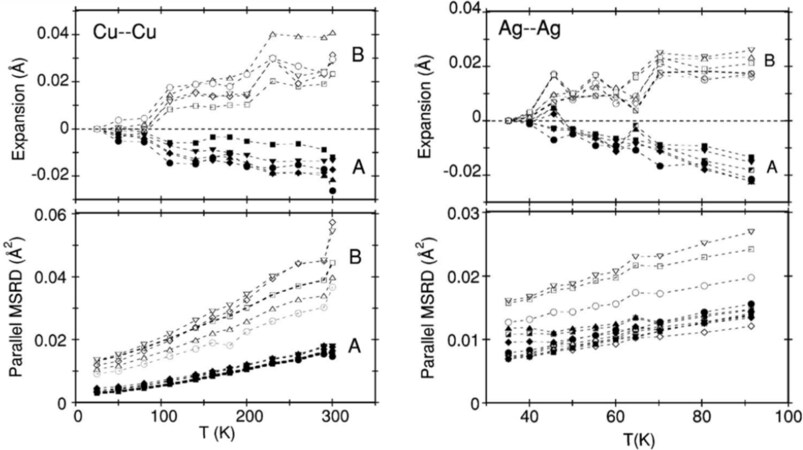
Figure 15. Bond thermal expansion (top panels) and parallel MSRDs (bottom panels) of the M-M second-shell distance in Cu
More recently, a number of crystals with the diamond-zincblende structure (Ge, CuCl, CdTe, InP and GaAs), affected by NTE at low temperatures, have been investigated by EXAFS[21, 32, 33, 37, 108]. These studies showed that a correlation exists between the strength of NTE, the degree of bond ionicity and some of the parameters determined from EXAFS analysis, such as the anisotropy of the relative vibrations of nearest-neighbor pairs.
Direct experimental evidence of the NTE mechanism in ScF
Figure 16. (A) Parallel MSRDs, (B) perpendicular MSRDs and (C) anisotropy of the relative thermal vibrations for the Sc-F and Sc-Sc atomic pairs determined by EXAFS in ScF
EXAFS was also employed to study the local dynamics of Prussian blue analogues (PBAs), an important family of multifunctional materials with applications in catalysis, energy storage, magnetism, drug delivery and so on[112]. In particular, some PBAs display NTE properties[113]. The chemical composition MM'(CN)
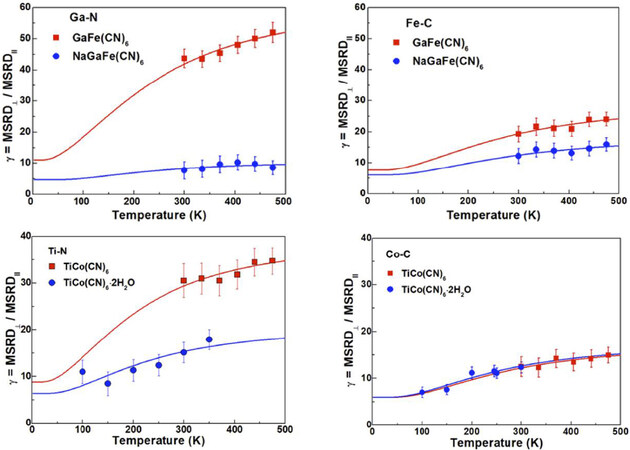
Figure 17. Parallel and perpendicular MSRDs for the Ga-N and Fe-C bonds [panels (A) and (B), respectively] of GaFe(CN)
Very interesting is the fact that the insertion of guest ions or molecules in PBA structures can inhibit NTE, thereby opening the possibility of controlling the thermal expansion of materials. For examples, the incorporation of K
Figure 18. Anisotropy of relative thermal vibrations determined by EXAFS in Na: GaFe(CN)
Superconducting materials
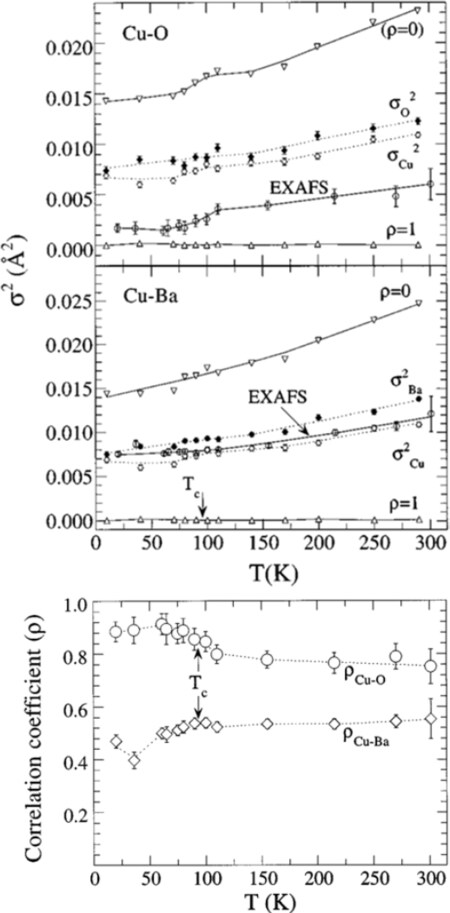
EXAFS was used to study superconducting materials. Lanzara et al.[120] studied the local atomic correlations in the HgBa
Figure 19. Temperature dependence of the EXAFS Debye-Waller factors (MSRDs) for the Cu-O and Cu-Ba atomic pairs in HgBa
More recently, Joseph et al.[121] studied the iron-oxypnictide superconductor system as a function of temperature. EXAFS showed a weak temperature and F-substitution dependence of the Fe-As bond length, in agreement with the strong covalent nature of this bond. More importantly, the temperature dependence of the Fe-As MSRDs was found to follow the correlated Einstein model, but with different Einstein frequencies for the superconducting and non-superconducting samples, with a hardening of the Fe-As bond in the former compared to the latter. This finding shows the non-negligible role of the lattice vibrational modes in the superconductivity of pnictide superconductors. This conclusion was supported by Chu et al.[122], who studied the Fe isotopic effect in the (Ba, K)Fe
Other applications
EXAFS allows for the exploration of a wide range of topics in condensed-matter physics and materials science. Before concluding, some more examples of EXAFS applications in studying local dynamics are presented.
EXAFS is widely used to study the structural and dynamic aspects of magnetic, ferroelectric and multiferroic materials, as well as of glasses and amorphous systems. Yokoyama et al.[127] studied the spin-crossover transition of a chain Fe(II) complex by temperature-dependent EXAFS and found an abrupt change in the first-shell Fe-N bond distance and the Debye-Waller factor at the transition temperature. The variation of the effective force constant for the Fe-N stretching vibration revealed a significant weakening of the Fe-N bond in the high-spin state. Later, the same authors investigated the anharmonicity and quantum effects in the Invar alloy Fe
Fischer et al.[130] detected the antiferrodistortive transition in perovskite SrTiO
Regarding glass and amorphous systems, in one of the pioneering works, Yang et al.[134] used temperature-dependent EXAFS to provide information about the nature and strength of local bonds of arsenic and arsenic-chalcogen compounds. They found that the As-As bonds in c-As are weaker than those in a-As, while the stretching forces of the As-S bonds in crystalline and glass As
The examples given in this section are clearly not exhaustive and other EXAFS studies of local dynamics can be found in the literature.
CONCLUSION
This paper has presented a brief review on the potential of EXAFS for the study of the local vibrational dynamics in materials. The strength of EXAFS is the selectivity of the atomic species and the sensitivity to short-range order and correlation of atomic motion.
The EXAFS approach, based on the cumulant expansion, gives information on the distribution of distances between the atoms of the absorbing species and their nearest neighbors, including the deviations from a Gaussian shape. In addition to giving information on the distance distribution and the anharmonicity of the interatomic potential, the EXAFS cumulants provide information on the local vibrational dynamics. Specifically, the first cumulant, benefitting from the difference between EXAFS and diffraction, leads to the evaluation of the perpendicular MSRD, while the second cumulant corresponds, in good approximation, to the parallel MSRD. The anisotropy of the relative thermal vibrations can thus be determined by EXAFS.
Some information has been provided regarding the data analysis strategy in order to improve the EXAFS results. In particular, the binding energy
Finally, in order to show the capability of EXAFS to study the local dynamics, several examples of application have been reported, ranging over a wide array of topics. This work encourages the use of EXAFS spectroscopy as a dynamic probe and not only as a structural probe.
DECLARATIONS
Authors' contributions
The author contributed solely to the article.
Availability of data and materials
Not applicable.
Financial support and sponsorship
None.
Conflicts of interest
The author declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author (s) 2021.
REFERENCES
2. Artioli G. Atomic displacement parameters from diffraction studies. In: Gramaccioli CM, Papp G, Weiszburg T, editors. Energy modelling in minerals. budapest: mineralogical society of Great Britain and Ireland; 2002. pp. 389-405.
3. Wood IG, Knight KS, Price GD, Stuart JA. Thermal expansion and atomic displacement parameters of cubic KMgF3 perovskite determined by high-resolution neutron powder diffraction. J Appl Crystallogr 2002;35:291-5.
4. Denisov VN, Ivlev AN, Lipin AS, Mavrin BN, Orlov VG. Raman spectra and lattice dynamics of single-crystal. J Phys: Condens Matter 1997;9:4967-78.
5. Maczka M, Hanuza J, Paraguassu W, Gomes Souza Filho A, Tarso Cavalcante Freire P, Mendes Filho J. Phonons in ferroelectric Bi2WO6: Raman and infrared spectra and lattice dynamics. Appl Phys Lett 2008;92:112911.
6. Birman JL. Theory of crystal space groups and infra-red and raman lattice processes of insulating crystals. Theory of crystal space groups and lattice dynamics. Berlin: Springer Berlin Heidelberg; 1984. pp. 1-521.
7. Strauch D, Pavone P, Mayer AP, et al. Ab initio lattice dynamics: methods, results, and applications. In: Helbig R, editor. Advances in solid state physics 37. Berlin: Springer Berlin Heidelberg; 1998. pp. 99-124.
8. Gonze X, Rignanese G, Caracas R. First-principle studies of the lattice dynamics of crystals, and related properties. Zeitschrift für Kristallographie - Crystalline Materials 2005;220:458-72.
9. Dove MT. Some fundamentals. Introduction to Lattice Dynamics. Cambridge University Press; 2010. pp. 1-17.
10. Albertsson J, Abrahams SC, Kvick Å. Atomic displacement, anharmonic thermal vibration, expansivity and pyroelectric coefficient thermal dependences in ZnO. Acta Crystallogr B Struct Sci 1989;45:34-40.
11. Downs RT, Gibbs GV, Boisen MB. A study of the mean-square displacement amplitudes of Si, Al, and O atoms in framework structures; evidence for rigid bonds, order, twinning, and stacking faults. American Mineralogist 1990;75:1253-67.
12. Krisch M, Sette F. Inelastic X-Ray Scattering from Phonons. In: Cardona M, Merlin R, editors. Light scattering in solid IX. Berlin: Springer Berlin Heidelberg; 2006. pp. 317-70.
14. Dickens MH, Hutchings MT. Inelastic neutron scattering study of the phonon dispersion relation of PbF2 at 10K. J Phys C: Solid State Phys 1978;11:461-8.
16. Giarola M, Sanson A, Monti F, et al. Vibrational dynamics of anatase TiO2: Polarized Raman spectroscopy and ab initio calculations. Phys Rev B 2010;81.
17. Iliev MN, Lee H, Popov VN, et al. Raman- and infrared-active phonons in hexagonal YMnO3: Experiment and lattice-dynamical calculations. Phys Rev B 1997;56:2488-94.
18. Stern EA, Sayers DE, Lytle FW. Extended x-ray-absorption fine-structure technique. III. Determination of physical parameters. Phys Rev B 1975;11:4836-46.
19. Beni G, Platzman PM. Temperature and polarization dependence of extended x-ray absorption fine-structure spectra. Phys Rev B 1976;14:1514-8.
20. Fornasini P. Study of lattice dynamics via extended x-ray absorption fine structure. J Phys: Condens Matter 2001;13:7859-72.
21. Schnohr CS, Kluth P, Araujo LL, et al. Anisotropic vibrations in crystalline and amorphous InP. Phys Rev B 2009;79.
22. Dalba G, Fornasini P. EXAFS Debye-Waller factor and thermal vibrations of crystals. J Synchrotron Radiat 1997;4:243-55.
23. Teo B. Extended X-Ray Absorption Fine Structure (EXAFS) spectroscopy: techniques and applications. In: Teo BK, Joy DC, editors. EXAFS spectroscopy. Boston: Springer US; 1981. pp. 13-58.
24. Paufler PP. Introduction to XAFS. A practical guide to X-ray absorption fine structure spectroscopy. By Grant Bunker. p. viii + 260. Cambridge University Press, 2010. J Synchrotron Rad 2011;18:818.
25. Crozier RED, Rehr JJ, Ingalls R. X-ray absorption: principles, applications, techniques of exafs, sexafs, and xanes. New York: Wiley; 1988.
26. Hayes T, Boyce J. Extended x-ray absorption fine structure spectroscopy. Elsevier; 1983. pp. 173-351.
27. Henderson GS, de Groot FMF, Moulton BJA. X-ray absorption near-edge structure (XANES) spectroscopy. Reviews in Mineralogy and Geochemistry 2014;78:75-138.
29. Bunker G. Application of the ratio method of EXAFS analysis to disordered systems. Nucl Instrum Methods Phys Res A 1983;207:437-44.
30. Fornasini P, Monti F, Sanson A. On the cumulant analysis of EXAFS in crystalline solids. J Synchrotron Radiat 2001;8:1214-20.
31. Busing WR, Levy HA. The effect of thermal motion on the estimation of bond lengths from diffraction measurements. Acta Cryst 1964;17:142-6.
32. Vaccari M, Grisenti R, Fornasini P, Rocca F, Sanson A. Negative thermal expansion in CuCl: an extended x-ray absorption fine structure study. Phys Rev B 2007;75.
33. Ahmed SI, Aquilanti G, Novello N, Olivi L, Grisenti R, Fornasini P. Local vibrational properties of GaAs studied by extended X-ray absorption fine structure. J Chem Phys 2013;139:164512.
34. Yoshiasa A, Koto K, Maeda H, Ishii T. The mean-square relative displacement and displacement correlation functions in tetrahedrally and octahedrally coordinated A(N)B(8-N) crystals. Jpn J Appl Phys 1997;36:781-4.
35. Sanson A, Rocca F, Dalba G, et al. Negative thermal expansion and local dynamics in Cu2O and Ag2O. Phys Rev B 2006;73.
36. Fornasini P, a Beccara S, Dalba G, et al. Extended x-ray-absorption fine-structure measurements of copper: local dynamics, anharmonicity, and thermal expansion. Phys Rev B 2004;70.
37. Dalba G, Fornasini P, Grisenti R, Purans J. Sensitivity of extended x-ray-absorption fine structure to thermal expansion. Phys Rev Lett 1999;82:4240-3.
38. Sanson A. Local dynamical properties of crystalline germanium and their effects in extended x-ray absorption fine structure. Phys Rev B 2010;81.
39. Cusack NE, Stein DL. The physics of structurally disordered matter: an introduction. Physics Today 1988;41:110-2.
40. Tranquada JM, Ingalls R. Extended x-ray - absorption fine-structure study of anharmonicity in CuBr. Phys Rev B 1983;28:3520-8.
41. Stern EA, Livns P, Zhang Z. Thermal vibration and melting from a local perspective. Phys Rev B Condens Matter 1991;43:8850-60.
42. Dalba G, Fornasini P, Grisenti R, Pasqualini D, Diop D, Monti F. Anharmonicity effects on the extended x-ray-absorption fine structure: the case of cadmium selenide. Phys Rev B 1998;58:4793-802.
43. Sanson A. Bond thermal expansion and effective pair potential in crystals: the case of cadmium selenide. J Phys Condens Matter 2011;23:315401.
44. Comaschi T, Balerna A, Mobilio S. Thermal dependent anharmonicity effects on gold bulk studied by extended x-ray-absorption fine structure. J Phys Condens Matter 2009;21:325404.
45. Kamishima O, Ishii T, Maeda H, Kashino S. EXAFS study on temperature dependence of nearest neighbor distance in CuBr. Solid State Communications 1997;103:141-4.
46. Dalba G, Fornasini P, Gotter R, Rocca F. Anharmonicity effects on the extended x-ray-absorption fine structure: the case of beta -AgI. Phys Rev B Condens Matter 1995;52:149-57.
47. Frenkel AI, Rehr JJ. Thermal expansion and x-ray-absorption fine-structure cumulants. Phys Rev B Condens Matter 1993;48:585-8.
48. Yokoyama T. Path-integral effective-potential theory for EXAFS cumulants compared with the second-order perturbation. J Synchrotron Radiat 1999;6:323-5.
49. Van Hung N, Rehr JJ. Anharmonic correlated Einstein-model Debye-Waller factors. Phys Rev B 1997;56:43-6.
50. Van Hung N, Fornasini P. Anharmonic effective potential, correlation effects, and EXAFS cumulants calculated from a morse interaction potential for fcc metals. J Phys Soc Jpn 2007;76:084601.
51. Hung NV, Tien TS, Duc NB, Vuong DQ. High-order expanded XAFS Debye-Waller factors of HCP crystals based on classical anharmonic correlated Einstein model. Mod Phys Lett B 2014;28:1450174.
52. Vila FD, Lindahl VE, Rehr JJ. X-ray absorption Debye-Waller factors from ab initio molecular dynamics. Phys Rev B 2012;85.
53. Miyanaga T, Fujikawa T. Quantum statistical approach to Debye-Waller factors in EXAFS, EELS and ARXPS. VI. Path-integral approach to morse potential systems. J Phys Soc Jpn 1998;67:2930-7.
54. Rehr JJ, Albers RC. Theoretical approaches to x-ray absorption fine structure. Rev Mod Phys 2000;72:621-54.
55. Rehr JJ, Kas JJ, Vila FD, Prange MP, Jorissen K. Parameter-free calculations of X-ray spectra with FEFF9. Phys Chem Chem Phys 2010;12:5503-13.
56. Purans J, Afify ND, Dalba G, et al. Isotopic effect in extended x-ray-absorption fine structure of germanium. Phys Rev Lett 2008;100:055901.
57. Sanson A. Isotopic effect on the local dynamics of crystalline germanium. Solid State Sciences 2010;12:1988-92.
58. Yokoyama T, Ohta T, Sato H. Thermal expansion and anharmonicity of solid Kr studied by extended x-ray-absorption fine structure. Phys Rev B 1997;55:11320-9.
59. Sanson A. On the neglecting of higher-order cumulants in EXAFS data analysis. J Synchrotron Radiat 2009;16:864-8.
60. Jeong I, Heffner RH, Graf MJ, Billinge SJL. Lattice dynamics and correlated atomic motion from the atomic pair distribution function. Phys Rev B 2003;67.
61. Beccara SA, Fornasini P. Path-integral Monte Carlo calculation of the effects of thermal disorder in extended x-ray-absorption fine structure of copper. Phys Rev B 2008;77.
62. Maradudin AA, Montroll EW, Weiss GH, Ipatova IP. Theory of lattice dynamics in the harmonic approximation. New York: Academic Press; 1971.
63. Sevillano E, Meuth H, Rehr JJ. Extended x-ray absorption fine structure Debye-Waller factors. I. Monatomic crystals. Phys Rev B 1979;20:4908-11.
64. Vaccari M, Fornasini P. Einstein and Debye models for EXAFS parallel and perpendicular mean-square relative displacements. J Synchrotron Radiat 2006;13:321-5.
65. Hu L, Chen J, Sanson A, et al. New insights into the negative thermal expansion: direct experimental evidence for the “Guitar-String” effect in cubic ScF3. J Am Chem Soc 2016;138:8320-3.
66. Li CW, Tang X, Muñoz JA, et al. Structural relationship between negative thermal expansion and quartic anharmonicity of cubic ScF3. Phys Rev Lett 2011;107:195504.
67. Sanson A. On the Einstein model for EXAFS parallel and perpendicular mean-square relative displacements. J Synchrotron Radiat 2008;15:514-8.
68. Timoshenko J, Anspoks A, Kalinko A, Kuzmin A. Local structure and dynamics of wurtzite-type ZnO from simulation-based EXAFS analysis: local structure and dynamics of wurtzite-type ZnO from simulation-based EXAFS analysis. Phys Status Solidi C 2014;11:1472-5.
69. Jonane I, Lazdins K, Timoshenko J, et al. Temperature-dependent EXAFS study of the local structure and lattice dynamics in cubic Y2O3. J Synchrotron Radiat 2016;23:510-8.
70. Timoshenko J, Kuzmin A, Purans J. Molecular dynamics simulations of EXAFS in germanium. Open Physics 2011;9.
71. Yokoyama T. Path-integral effective-potential method applied to extended x-ray-absorption fine-structure cumulants. Phys Rev B 1998;57:3423-32.
72. Beccara S, Dalba G, Fornasini P, et al. Local thermal expansion in copper: Extended x-ray-absorption fine-structure measurements and path-integral Monte Carlo calculations. Phys Rev B 2003;68.
73. Palmer BJ, Pfund DM, Fulton JL. Direct modeling of EXAFS spectra from molecular dynamics simulations. J Phys Chem 1996;100:13393-8.
74. Price SWT, Zonias N, Skylaris C, Hyde TI, Ravel B, Russell AE. Fitting EXAFS data using molecular dynamics outputs and a histogram approach. Phys Rev B 2012;85.
75. Kuzmin A, Efimov V, Efimova E, Sikolenko V, Pascarelli S, Troyanchuk I. Interpretation of the Co K-edge EXAFS in LaCoO3 using molecular dynamics simulations. Solid State Ionics 2011;188:21-4.
76. Bocharov D, Krack M, Rafalskij Y, Kuzmin A, Purans J. Ab initio molecular dynamics simulations of negative thermal expansion in ScF3: the effect of the supercell size. Computational Materials Science 2020;171:109198.
77. Sanson A. Toward an understanding of the local origin of negative thermal expansion in ZrW2O8: limits and inconsistencies of the tent and rigid unit mode models. Chem Mater 2014;26:3716-20.
78. Bocharov D, Anspoks A, Timoshenko J, Kalinko A, Krack M, Kuzmin A. Interpretation of the Cu K-edge EXAFS spectra of Cu3N using ab initio molecular dynamics. Radiation Physics and Chemistry 2020;175:108100.
79. Roscioni OM, Zonias N, Price SWT, Russell AE, Comaschi T, Skylaris C. Computational prediction of L3 EXAFS spectra of gold nanoparticles from classical molecular dynamics simulations. Phys Rev B 2011;83.
80. Mierzwa B. EXAFS studies of bimetallic palladium-cobalt nanoclusters using Molecular Dynamics simulations. J Alloys Compd 2005;401:127-34.
81. Anspoks A, Kuzmin A. Interpretation of the Ni K-edge EXAFS in nanocrystalline nickel oxide using molecular dynamics simulations. J Non Cryst Solids 2011;357:2604-10.
82. Rybicki J, Rybicka A, Witkowska A, et al. The structure of lead-silicate glasses: molecular dynamics and EXAFS studies. J Phys: Condens Matter 2001;13:9781-97.
83. Rossano S, Ramos A, Delaye JM, et al. Iron surrounding in CaO-FeO-2SiO2 glass: EXAFS and molecular dynamics simulation. J Synchrotron Radiat 1999;6:247-8.
84. Dziegielewski P, Mathon O, Kantor I, et al. High pressure atomic structure of Zr-Cu metallic glass via EXAFS spectroscopy and molecular dynamics simulations. High Pressure Research 2020;40:54-64.
85. Migliorati V, Serva A, Aquilanti G, et al. Combining EXAFS spectroscopy and molecular dynamics simulations to understand the structural and dynamic properties of an imidazolium iodide ionic liquid. Phys Chem Chem Phys 2015;17:2464-74.
86. Serva A, Migliorati V, Spezia R, D’Angelo P. How does CeIII nitrate dissolve in a protic ionic liquid? a combined molecular dynamics and EXAFS study. Chemistry 2017;23:8424-33.
87. Busato M, Lapi A, D’Angelo P, Melchior A. Coordination of the Co2+ and Ni2+ ions in Tf2N- based ionic liquids: a combined x-ray absorption and molecular dynamics study. J Phys Chem B 2021;125:6639-48.
88. Rockenberger J, Tröger L, Kornowski A, et al. EXAFS studies on the size dependence of structural and dynamic properties of CdS nanoparticles. J Phys Chem B 1997;101:2691-701.
89. Araujo LL, Kluth P, de M. Azevedo G, Ridgway MC. Vibrational properties of Ge nanocrystals determined by EXAFS. Phys Rev B 2006;74.
90. Gilbert B, Huang F, Zhang H, Waychunas GA, Banfield JF. Nanoparticles: strained and stiff. Science 2004;305:651-4.
91. Rockenberger J, Tröger L, Rogach AL, et al. The contribution of particle core and surface to strain, disorder and vibrations in thiolcapped CdTe nanocrystals. J Chem Phys 1998;108:7807-15.
92. Sprouster DJ, Giulian R, Araujo LL, et al. Structural and vibrational properties of Co nanoparticles formed by ion implantation. J Appl Phys 2010;107:014313.
93. Comaschi T, Balerna A, Mobilio S. Temperature dependence of the structural parameters of gold nanoparticles investigated with EXAFS. Phys Rev B 2008;77.
94. Li WH, Wu SY, Yang CC, et al. Thermal contraction of au nanoparticles. Phys Rev Lett 2002;89:135504.
95. Duan Z, Li Y, Timoshenko J, et al. A combined theoretical and experimental EXAFS study of the structure and dynamics of Au147 nanoparticles. Catal Sci Technol 2016;6:6879-85.
96. Timoshenko J, Duan Z, Henkelman G, Crooks RM, Frenkel AI. Solving the structure and dynamics of metal nanoparticles by combining X-Ray absorption fine structure spectroscopy and atomistic structure simulations. Annu Rev Anal Chem (Palo Alto Calif) 2019;12:501-22.
97. Hu L, Qin F, Sanson A, et al. Localized symmetry breaking for tuning thermal expansion in ScF3 nanoscale frameworks. J Am Chem Soc 2018;140:4477-80.
98. Mary TA, Evans JSO, Vogt T, Sleight AW. Negative thermal expansion from 0.3 to 1050 Kelvin in ZrW2O8. Science 1996;272:90-2.
99. Cai W, Katrusiak A. Giant negative linear compression positively coupled to massive thermal expansion in a metal-organic framework. Nat Commun 2014;5:4337.
100. Chen J, Hu L, Deng J, Xing X. Negative thermal expansion in functional materials: controllable thermal expansion by chemical modifications. Chem Soc Rev 2015;44:3522-67.
101. Cao D, Bridges F, Kowach GR, Ramirez AP. Frustrated soft modes and negative thermal expansion in ZrW2O8. Phys Rev Lett 2002;89:215902.
102. Cao D, Bridges F, Kowach GR, Ramirez AP. Correlated atomic motions in the negative thermal expansion material ZrW2O8: a local structure study. Phys Rev B 2003;68.
103. Beccara S, Dalba G, Fornasini P, Grisenti R, Sanson A, Rocca F. Local thermal expansion in a cuprite structure: the case of Ag(2)O. Phys Rev Lett 2002;89:025503.
104. Dapiaggi M, Tiano W, Artioli G, Sanson A, Fornasini P. The thermal behaviour of cuprite: An XRD-EXAFS combined approach. Nucl Instrum Methods Phys Res B 2003;200:231-6.
105. Hammonds KD, Dove MT, Giddy AP, Heine V, Winkler B. Rigid-unit phonon modes and structural phase transitions in framework silicates. American Mineralogist 1996;81:1057-79.
106. Sanson A. Tension effect in local dynamics of cuprite structures. Solid State Sciences 2009;11:1489-93.
107. Abd el All N, Dalba G, Diop D, et al. Negative thermal expansion in crystals with the zincblende structure: an EXAFS study of CdTe. J Phys Condens Matter 2012;24:115403.
108. Barrera GD, Bruno JAO, Barron THK, Allan NL. Negative thermal expansion. J Phys: Condens Matter 2005;17:R217-52.
109. Qin F, Chen J, Aydemir U, et al. Isotropic zero thermal expansion and local vibrational dynamics in (Sc,Fe)F3. Inorg Chem 2017;56:10840-3.
110. Purans J, Fornasini P, Ali SE, Dalba G, Kuzmin A, Rocca F. X-ray absorption spectroscopy study of local dynamics and thermal expansion in ReO3. Phys Rev B 2015;92.
111. Zakaria MB, Chikyow T. Recent advances in Prussian blue and Prussian blue analogues: synthesis and thermal treatments. Coordination Chemistry Reviews 2017;352:328-45.
112. Chapman KW, Chupas PJ, Kepert CJ. Compositional dependence of negative thermal expansion in the prussian blue analogues MIIPtIV(CN)6 (M: Mn, Fe, Co, Ni, Cu, Zn, Cd). ChemInform 2006;37.
113. Gao Q, Shi N, Sun Q, et al. Low-frequency phonon driven negative thermal expansion in cubic GaFe(CN)6 prussian blue analogues. Inorg Chem 2018;57:10918-24.
114. Shi N, Gao Q, Sanson A, et al. Negative thermal expansion in cubic FeFe(CN)6 Prussian blue analogues. Dalton Trans 2019;48:3658-63.
115. Gao Q, Sun Y, Shi N, et al. Large isotropic negative thermal expansion in water-free Prussian blue analogues of ScCo(CN)6. Scripta Materialia 2020;187:119-24.
116. Gao Q, Chen J, Sun Q, et al. Switching between giant positive and negative thermal expansions of a YFe(CN)6-based prussian blue analogue induced by guest species. Angew Chem Int Ed Engl 2017;56:9023-8.
117. Gao Q, Shi N, Sanson A, et al. Tunable thermal expansion from negative, zero, to positive in cubic prussian blue analogues of GaFe(CN)6. Inorg Chem 2018;57:14027-30.
118. Gao Q, Shi X, Venier A, et al. Effect of H2O molecules on thermal expansion of TiCo(CN)6. Inorg Chem 2020;59:14852-5.
119. Lanzara A, Saini NL, Bianconi A, Duc F, Bordet P. Anomalous local atomic correlations in HgBa2CuO4+δ. Phys Rev B 1999;59:3851-4.
120. Joseph B, Iadecola A, Malavasi L, Saini NL. Temperature-dependent local structure of NdFeAsO(1-x)F(x) system using arsenic K-edge extended x-ray absorption fine structure. J Phys Condens Matter 2011;23:265701.
121. Chu W, Cheng J, Chu S, et al. Iron isotope effect and local lattice dynamics in the (Ba, K)Fe2As2 Superconductor studied by temperature-dependent EXAFS. Sci Rep 2013;3.
122. Paris E, Simonelli L, Wakita T, et al. Temperature dependent local atomic displacements in ammonia intercalated iron selenide superconductor. Sci Rep 2016;6:27646.
123. Saini NL, Oyanagi H, Ito T, et al. Temperature dependent local Cu-O displacements from underdoped to overdoped La-Sr-Cu-O superconductor. The European Physical Journal B - Condensed Matter 2003;36:75-80.
124. Saini NL, Filippi M, Oyanagi H, Ihara H, Iyo A, Bianconi A. Temperature-dependent local structure in the Nb3Ge superconductor studied by high-resolution Ge K -edge EXAFS measurements. Phys Rev B 2003;68.
125. Chu WS, Zhang S, Yu MJ, et al. Correlation between local vibrations and metal mass in AlB2-type transition-metal diborides. J Synchrotron Radiat 2009;16:30-7.
126. Yokoyama T, Murakami Y, Kiguchi M, Komatsu T, Kojima N. Spin-crossover phase transition of a chain Fe(II) complex studied by x-ray-absorption fine-structure spectroscopy. Phys Rev B 1998;58:14238-44.
127. Yokoyama T, Eguchi K. Anharmonicity and quantum effects in thermal expansion of an Invar alloy. Phys Rev Lett 2011;107:065901.
128. Panchwanee A, Schiesaro I, Mobilio S, et al. An evidence of local structural disorder across spin-reorientation transition in DyFeO3: an extended x-ray absorption fine structure (EXAFS) study. J Phys Condens Matter 2019;31:345403.
129. Fischer M, Lahmar A, Maglione M, et al. Local disorder studied in SrTiO3 at low temperature by EXAFS spectroscopy. Phys Rev B Condens Matter 1994;49:12451-6.
130. Sanson A, Mathon O, Pascarelli S. Local vibrational dynamics of hematite (α-Fe2O3) studied by extended x-ray absorption fine structure and molecular dynamics. J Chem Phys 2014;140:224504.
131. Miyanaga T, Diop D, Ikeda S, Kon H. Study of the local structure changes in PbTiO 3 by Pb L III EXAFS. Ferroelectrics 2002;274:41-53.
132. Subías G, García J, Blasco J, Proietti MG. Local structure at the manganese site in mixed-valence manganites. Phys Rev B 1998;57:748-54.
133. Yang CY, Paesler MA, Sayers DE. Determination of bond strengths of arsenic and arsenic chalcogen compounds using the temperature dependence of extended x-ray-absorption fine structure. Phys Rev B Condens Matter 1987;36:980-8.
134. Sanson A, Rocca F, Armellini C, Ahmed S, Grisenti R. Local study on the MoO4 units in AgI-doped silver molybdate glasses. J Non Cryst Solids 2008;354:94-7.
135. Sanson A, Rocca F, Dalba G, Fornasini P, Grisenti R. Influence of temperature on the local structure around iodine in fast-ion-conducting AgI:Ag2 MoO4 glasses. New J Phys 2007;9:88.
136. Siqueira MC, Maia RN, Araujo RM, Machado KD, Stolf SF. Structural and thermal investigations of an amorphous GaSe9 alloy using EXAFS, cumulant expansion, and reverse Monte Carlo simulations. J Chem Phys 2015;142:054504.
137. Yoshitake H, Sugihara T, Tatsumi T. XAFS study on the local structure of Ti in amorphous mesoporous titania. Phys Chem Chem Phys 2003;3:767-72.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Sanson A. EXAFS spectroscopy: a powerful tool for the study of local vibrational dynamics. Microstructures 2021;1:2021004. http://dx.doi.org/10.20517/microstructures.2021.03
AMA Style
Sanson A. EXAFS spectroscopy: a powerful tool for the study of local vibrational dynamics. Microstructures. 2021; 1(1): 2021004. http://dx.doi.org/10.20517/microstructures.2021.03
Chicago/Turabian Style
Sanson, Andrea. 2021. "EXAFS spectroscopy: a powerful tool for the study of local vibrational dynamics" Microstructures. 1, no.1: 2021004. http://dx.doi.org/10.20517/microstructures.2021.03
ACS Style
Sanson, A. EXAFS spectroscopy: a powerful tool for the study of local vibrational dynamics. Microstructures. 2021, 1, 2021004. http://dx.doi.org/10.20517/microstructures.2021.03
About This Article
Copyright
Data & Comments
Data
 Cite This Article 36 clicks
Cite This Article 36 clicks




















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.