Commentary on “Heterogenous nature of enhanced piezoelectricity in relaxor-ferroelectric crystals”

Enhanced piezoelectricity in Pb-based perovskite ferroelectric single crystals has been of research interest for about 30 years since the early reports by Uchino^[1] of high weak-field properties (d33~1500 pC/N) to subsequent ones by Park et al.^[2] of large field-induced strains (ε = 1.5%, E = 120 kV/cm). The fundamental scientific question of what causes the enhanced piezoelectricity of the Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃ (PMN-PT) or Pb(Zn_1/3Nb_2/3)O₃-PbTiO₃ (PZN-PT) type piezoelectric crystals naturally arose, as it has the potential to help guide ultrahigh piezoelectricity by design.

In the United States, under the support of the Office of Naval Research or ONR (Smith), much effort was expended to develop a theory of intermediate monoclinic (M) phases that structurally bridge rhombohedral (R) and tetragonal (T) ones across the morphotropic phase boundary (MPB)^[3]. Ab-initio approaches predicted a monoclinic unit cell, indicating an intermediate M phase that is structurally homogeneous. The polarization vector within the unit cell rotated on application of electric field E, resulting in electromechanical transduction.

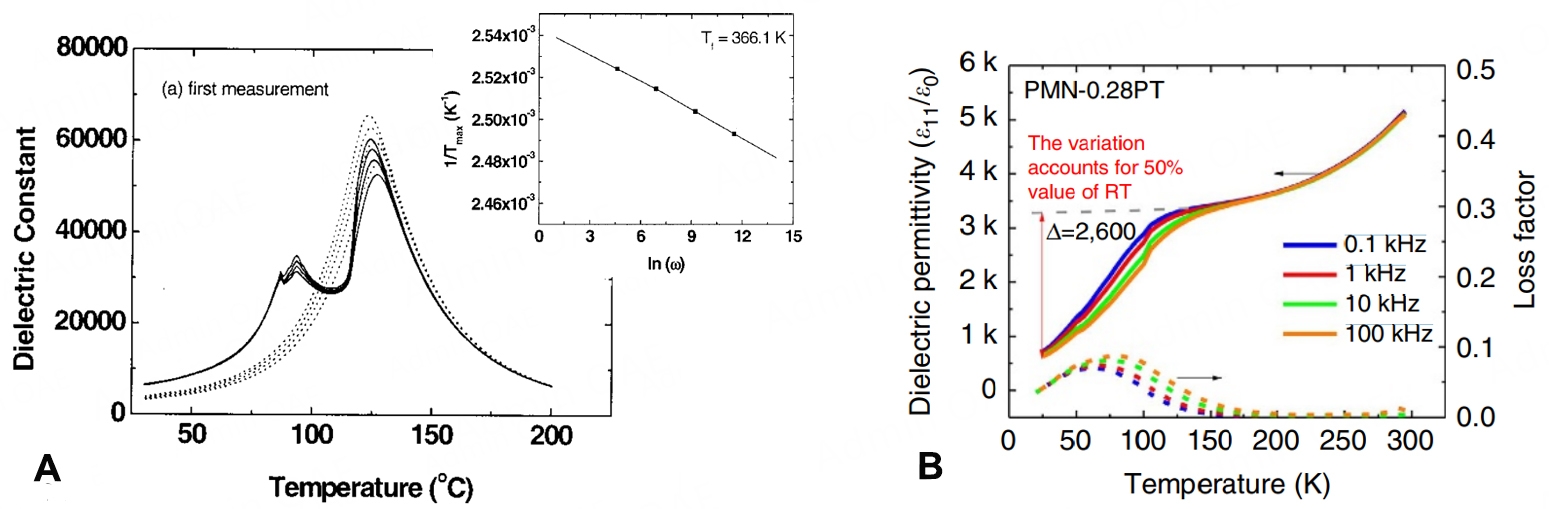
However, it must be remembered that the perovskite crystals which exhibit ultrahigh piezoelectricity are in solid solutions between end members having relaxor and normal ferroelectric behaviors. Relaxors are unique in that they are characterized by a structural heterogeneity of lower symmetry within an average cubic state^[4]. Figure 1A shows data taken from the same (001) PMN-32at%PT crystal under different electrical histories. In the annealed condition (dotted lines)^[5], typical relaxor ferroelectric behavior is observed, where the temperature of the dielectric maximum (T_max) is frequency dependent. Analysis of the frequency dependence of T_max with the Vogel-Fulcher equation (see insert) yielded a freezing temperature of Tf = 366 K. Electric field cooling (FC) results in the emergence of a long-range ordered ferroelectric state that remains stable on the removal of E. On subsequent reheating under E = 0 from a previously FC state, a macrodomain to polar nanoregion transition occurs near Tf, somewhat similar to earlier reports by Yao et al.^[6] for PLZT ceramics. Clearly, in these complex relaxor crystals, length scales are important to the structure-property relations and the average symmetry itself.

Figure 1. (A) Temperature-dependent dielectric response in the range above 300 K for a <001>- oriented PMN–PT crystal on heating from a poled condition under zero field, and subsequent re-cooling. The insert shows a Vogel-Fulcher fit to the frequency dependence of the dielectric constant in the zero-field cooled measurement. Reproduced with permission^[5]. Copyright 2001 AIP Publishing LLC. (B) Temperature-dependent dielectric response in the range below 300 K for a <001> PMN-PT crystal on zero-field heating from a poled condition. Reproduced with permission^[18]. Copyright 2016 Nature Publishing Group.

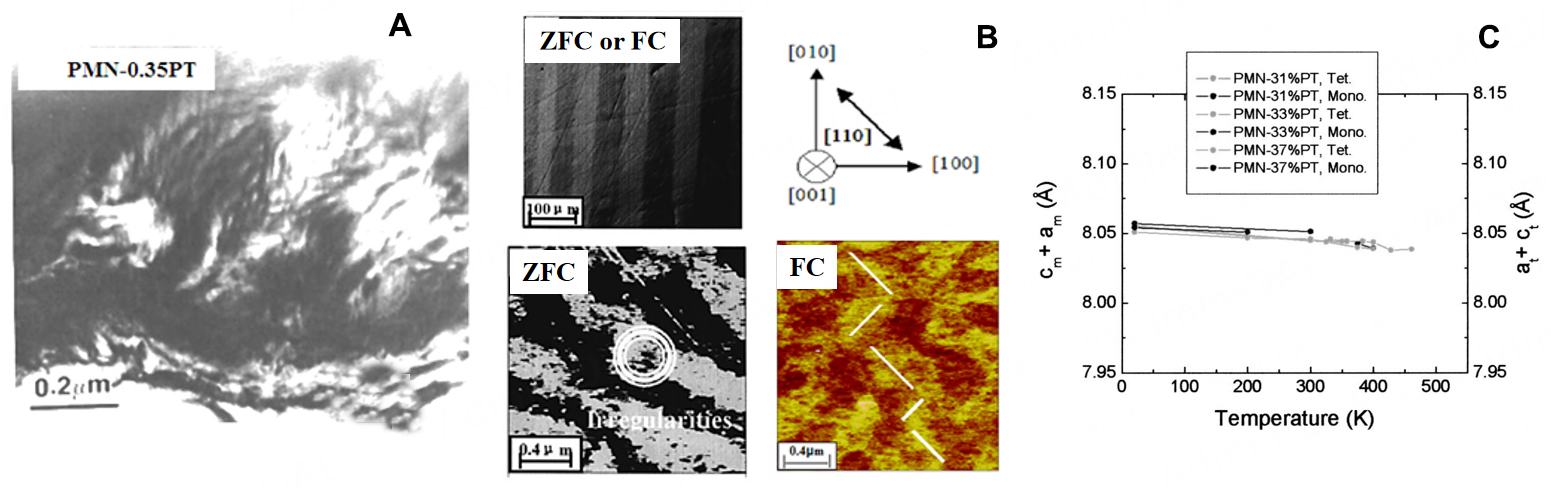
Other evidence exists supporting the proposition that the heterogeneous concept of relaxors can be extended to the poled piezoelectric state. Early electron microscopy studies by Randall et al. in 1987 demonstrated the existence of polar nanoregions in relaxors^[7]. Subsequent studies in 1994 revealed that the nanoregions assembled into tweed-like structures on approaching the MPB^[8], as shown in Figure 2A. In ferroelastic transformations, Khachaturyan has shown that tweed-like structures result in an apparent monoclinic MC structure^[9], even though the local symmetry is tetragonal. Modelling by Bratkovsky, Salje and Heine in 1994^[10] simulated the domain evolution pathway of elastic clusters to tweed microdomains. Kartha, Castan, Krumhansl and Sethna^[11] in 1991 showed using a Landau-Ginsburg approach that a tweed mesophase could be trapped to low temperatures due to nonlinear non-local elasticity coupled to quenched compositional inhomogeneity. In 2006^[12,13], piezo-force and polarized light microscopy studies of poled PMN-PT crystals revealed macrodomain plates having an internal fine (~200 nm) domain structure that was altered from a lamellar to zig-zag configuration under electric field application, as shown in Figure 2B. Finally, structural studies have shown that the thermodynamic phase space is quite flat^[14]: for a fixed electric field and composition, simply changing the direction along which E is applied can result in changes between induced monoclinic, orthorhombic, and tetragonal/ rhombohedral phases.

Figure 2. (A) Transmission electron microscopy image showing the presence of tweed-like structures in PMN-35PT. Reproduced with permission^[8]. Copyright 1995 AIP Publishing LLC. (B) Polarized light PLM (top) and piezo-force PFM microscopy (bottom) images. Reproduced with permission^[13]. Copyright 2005 AIP Publishing LLC. (C) Temperature dependence of the general invariance condition of equation (3.13). Reproduced with permission^[16]. Copyright 2003 AIP Publishing LLC.

Based on these experimental insights, a structurally heterogeneous model for the enhanced piezoelectricity of the PMN-PT type crystals was proposed^[15-17]. The work was also supported by ONR (Lindberg). It is based on the concept of a mesoscale mechanism, where polar nanoregion activity within a poled ferroelectric condition is responsible for enhanced piezoelectricity. The model was an extension of an adaptive phase theory for ferroelastic and martensitic transformations^[9] that was applied to ferroelectrics with large strain. Theoretically, it is based on the conformal miniaturization of domains with low domain wall energies that are stress-accommodating (i.e., tweed). Experimentally, this requires the existence of structurally heterogeneous regions of nanometer size. The spatial and geometric distribution of the nanoregions is then controlled by special and general invariant conditions that minimize the excess elastic energy. In the case of PMN-PT type piezoelectric crystals, averaging over an ensemble of tetragonal polar nanoregions results in an apparent monoclinic MC-type structure by diffraction. Likewise, averaging over an ensemble of rhombohedral polar nanoregions results in an apparent monoclinic MA-type structure. In the monoclinic MA and MC phases, the changes in the lattice parameter with temperature and field are invariant to the geometric conditions of the adaptive phase theory, as shown in Figure 2C. Both the structurally homogeneous and heterogenous models require the anisotropy of the polarization direction to be small. In the homogenous case, the polarization vector rotates at the unit cell level; whereas in the heterogenous case, there is a change in the distribution of the polar nanoregions between equivalent orientations.

This brings me to the point that this commentary would like to make. It concerns a brief comparison of another approach to the heterogeneous concept by Li et al. that was put forward some years after the adaptive phase theory^[18,19]. Let us be upfront and direct, the experimental observations that were cited in the preceding paragraph could equally provide support to either one of these heterogenous models, as the data reflects a critical role of the local structure on the average structure-property relations. The concept by Li et al. and the adaptive phase^[15-17] are on the same general page^[17,18]. It is only a question of details, many of which whose importance may not yet be realized, simply due to the predominance of investigations has focused on a conventional homogenous phase. Both approaches recognize the existence of polarization gradient terms in the Landau-Ginzburg (LG) phenomenology and the need to relax the elastic energy. Additionally, both approaches recognize the important role of the contribution of polar nanoregions within the average anisotropy set by the poling directions. A unique aspect of the adaptive phase theory that the LG theory cannot explain by itself is the observed special invariant conditions of the crystal lattice parameters.

Data reported by Li et al. shows that the dielectric constant in the poled piezoelectric state becomes strongly frequency dispersive at temperatures far below (ΔT = 250-350 K) the temperature of the dielectric maximum (T_max ≈ 400 K), as shown in Figure 1B^[18,19]. This result clearly demonstrates that polar nanoregion contributions begin to freeze out on cooling below 100 K in the poled piezoelectric phase. It is only in the temperature range between 100 K [Figure 1B] and the macrodomain to polar nanoregion transition (see Figure 1A) that the dielectric constant appears to be nondispersive. It is believed this enhanced polarization contribution in the poled condition is responsible for the high piezoelectricity of poled crystals^[20]. One could also expect such low-temperature behavior in glassy tweed meso-states due to a coupling between non-local elasticity and compositional inhomogeneity^[11].

The strength of the adaptive phase theory is in its simple elegance in making invariant the lattice parameter changes with temperature and field based on a crystallographic/geometric theory. The strength of the approach by Li et al. is in its ability to bring together numerous gradient contributions and elastic boundary conditions into a phase field theory that could be used for piezoelectricity by computational design^[18-20]. The overall weakness has been that the majority of research efforts have been devoted to investigations within the framework of a homogenous single-phase monoclinic structure. To date, monoclinic phases in these complex Pb-based perovskites have only been reported in polydomain materials - there has yet to be the finding of a single-domain single-crystal monoclinic phase.