Thermal expansion coefficient of monolayer MoS2 determined using temperature-dependent Raman spectroscopy combined with finite element simulations
Abstract
The thermal expansion coefficient is an important parameter of monolayer MoS2 that affects the performance of its related optoelectronic devices. To obtain the thermal expansion coefficient of monolayer MoS2, suspended and supported MoS2 are systematically investigated using micro-Raman spectroscopy in a temperature range of 77-557 K. Obvious differences in the temperature-dependent evolution of the Raman peaks between suspended and supported MoS2 are observed, which result from the thermal expansion coefficient mismatch between MoS2 and the substrate. With the help of the finite element method, the thermal strain in suspended and supported MoS2 is calculated and used to deduce the thermal expansion coefficient mismatch-induced Raman shift. By matching the simulation and experimental results, the thermal expansion coefficient of MoS2 is identified through the numerical inversion calculation. Our results demonstrate that the combination of micro-Raman spectroscopy and finite element simulations is highly effective for identifying the intrinsic thermal expansion coefficient of two-dimensional materials.
Keywords
Introduction
Transition metal dichlorides (TMDs) are a large class of two-dimensional layered materials with a natural band gap structure and have attracted increasing attention in the past decade[1-3]. Their intralayer atoms are bound by covalent bonds, while their interlayer atoms are coupled by weak van der Waals force. Each layer of a TMD is three atoms thick, with a triangular or hexagonal transition metal atomic plane sandwiched between two triangular layers of dichloride atoms[4,5]. Monolayer TMDs lack the inversion symmetry of the crystal space group and undergo a transition from an indirect to direct band gap[6,7]. MoS2 is a typical TMD material with a bulk indirect band gap of 1.29 eV and a direct band gap of 1.9 eV for monolayer MoS2. MoS2 has high carrier mobility and optical absorptivity, which give it promising applications in optoelectronic devices.
As a building block of nanodevices, monolayer MoS2 is attached to the substrate in practical applications. The differences in the thermal expansion coefficient (TEC) between the MoS2 layer and the substrate causes thermal strain inside the MoS2 layer. Because the self-heating effect cannot be avoided during the operation of devices, the thermal strain consequently induced by TEC mismatch should be taken into consideration when studying the electronic and transport properties of devices[8,9]. Thermal strain can affect the performance of devices and even results in cracking failure when it exceeds the bearing limit of MoS2[10]. Therefore, determining the TEC of monolayer MoS2 is important for its future application in devices.
However, direct measurement of the TEC of monolayer MoS2 is still hindered as it is attached to the substrate. Researchers have performed theoretical calculations to obtain the TEC of MoS2[11-14]. The positive linear TEC of two-dimensional (2D) MoS2 was estimated using first-principles based on the quasiharmonic approximation[11]. Ding et al.[12] used density functional perturbation theory (DFPT) to calculate the phonon spectra of 2H-MoS2 structures. Huang et al.[13] proposed a negative-positive crossover in the TEC of monolayer MoS2 at 20 K, which was attributed to the competition between the modes with negative and positive Grüneisen parameters.
Raman spectroscopy has been demonstrated to be a powerful tool for studying the microstructure and electronic properties of MoS2, including the layer number, stress, doping and so on[15-18]. In recent years, Raman spectroscopy has also been used to study the thermal parameters of MoS2[19]. Zhang et al.[20] obtained the TEC of monolayer MoS2 using a combination of theoretical and experimental methods and by characterizing the unique temperature dependence of the Raman peaks with three different substrates. Recently, the TEC of few-layer MoS2 was investigated by adopting suspended MoS2 as a freestanding sample[21]. However, absolute freestanding MoS2 cannot be achieved practically. Even when MoS2 is suspended on a hole or a groove, it is very difficult to observe the corresponding free expansion.
To our knowledge, previous studies of TEC have depended either on purely theoretical calculations or a combination of experimental characterization with first-principles modeling. In this work, we propose a new method to determine the TEC of MoS2 by combining the temperature-dependent Raman spectroscopy with finite element simulations. First, a systematic Raman study is carried out on suspended MoS2, compared with substrate-supported MoS2, in a temperature range from 77 to 557 K. The finite element method is then used to simulate the thermal strain caused by the TEC mismatch between the substrate and MoS2. The corresponding Raman frequency shift obtained by thermal mismatch is also calculated. By ensuring compatibility between the simulation and experimental results, the TEC of monolayer MoS2 is finally achieved by employing a numerical inversion method. Our work presents a simple method for assessing the TEC of monolayer MoS2, which can also be widely applied to study the thermophysical properties of many other 2D materials and thin films.
Materials and methods
Sample preparation
Monolayer MoS2 was obtained using a mechanical exfoliation method that has been demonstrated to be a feasible method for producing 2D materials[22]. This was then transferred onto a 300-nm-thick Si substrate that had been previously cleaned by oxygen plasma. Suspended MoS2 was achieved by transferring exfoliated MoS2 on periodic microhole arrays that was prefabricated on a SiO2/Si substrate by ultraviolet lithography and reactive ion etching technology. The microholes were 5 µm in diameter and 2 µm in depth. Monolayer MoS2 was roughly picked out by its color from optical microscopy and further identified using micro-Raman spectroscopy and atomic force microscopy.
Temperature-dependent raman measurements
Raman spectra were collected using a confocal micro-Raman spectrometer (Horiba HR Evolution). A solid-state laser with a wavelength of 532 nm was used as the excitation source. The laser beam was focused using a 50× long working distance objective with a numerical aperture of 0.5. The spot size was ~1.5 µm. To avoid the heating effect, the laser power was set to less than 1 mW. The sample was placed inside a cryostat cell (Linkam, THMS 600) and the temperature was changed from 77 to 557 K with an interval of 20 K.
Finite element simulations
According to the experimental environment of the sample in the low-temperature measurements, the mechanical thermal coupling analysis model was established by the finite element method. Two types of simulation models (supported and suspended MoS2) were built accordingly. As shown in Figure 1A, supported MoS2 is fully attached to the SiO2 substrate (SUP-MoS2). In contrast, suspended MoS2 covers the substrate with a microhole (SUS-MoS2), as shown in Figure 1B. The geometries of the models in the simulation were designed to match the real dimensions of the monolayer MoS2 and microhole fabricated. The diameter of the microhole was 5 µm and the periodicity was 8 µm. The thickness of monolayer MoS2 was set as 0.7 nm according to a previous study[23]. For the simplicity of the simulations, the thickness of the SiO2 layer was set as 100 nm, although the SiO2 layer in the real sample was 280 nm thick. The physical properties of SiO2 employed in the simulations were adopted from the built-in parameters in the software and are listed in Supplementary Table 1.
Figure 1. Schematic illustration of finite element model for (A) supported and (B) suspended MoS2.
In the modeling process, the mesh density was conventional and the maximum and minimum elements were 0.8 and 0.144 µm, respectively. The SiO2 base mapping and sweep function were obtained and the monolayer MoS2 was then mapped and swept. A layer of hexahedron meshes was obtained. It was assumed that the heating effect from the laser can be ignored. The sample was only subjected to the heat transfer response from the ambient temperature in the cryostat. In the process of the analysis and calculation, the solid mechanics and heat transfer module were coupled and transient analysis was adopted. The heat flux boundary condition was used in the solid heat transfer module. This convection heat flux can be described by the convection heat transfer equation:
where q0 represents the heat transfer from the environment to the model, h is the heat transfer coefficient, Text is the ambient temperature and T is the model temperature.
Results and discussion
Figure 2A exhibits the optical image of monolayer MoS2 transferred on a prepatterned SiO2/Si substrate with microholes. The typical Raman spectra for suspended and supported monolayer MoS2 at room temperature (293 K) and 77 K are presented in Figure 2B, in which two Raman modes can be seen clearly. The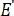 
mode originates from the in-plane vibration of molybdenum and sulfur atoms, while the 
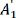mode represents the out-of-plane vibration[24]. Regarding the room-temperature spectrum of supported MoS2 (SUP-293 K), the 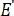mode is located at ~385.5 cm-1, whereas the 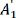mode is at ~404.5 cm-1. The frequency difference between the 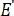and 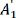modes is smaller than 20 cm-1, demonstrating that it is monolayer MoS2[25]. Moreover, the frequency differences between suspended and supported MoS2 are also observed in the room-temperature Raman spectra, which could be attributed to the internal strain caused during sample preparation[26].
Figure 2. (A) Optical microscopy image of monolayer MoS2 transferred on a prepatterned SiO2/Si substrate with 5 μm microholes. (B) Raman spectra of MoS2 collected at 77 and 293 K. (Solid lines represent SUP-MoS2 and the dotted line represents SUS-MoS2).
In addition to the room-temperature spectra, the Raman spectra of SUP-MoS2 and SUS-MoS2 collected at 77 K also exhibit differences. It is well known that the binding force from the substrate interferes with the deformation of the MoS2 film when the temperature changes because of the difference in the TEC of MoS2 and the SiO2 substrate. Although the experimental conditions are the same, supported and suspended MoS2 are subjected to different strain conditions and the deformation in the microstructure of MoS2 is different as a result. Consequently, the corresponding atomic lattice vibration is affected by the substrate. Figure 3 presents the Raman spectra of supported and suspended MoS2 at selected temperatures. With increasing temperature, an obvious redshift and broadening of the Raman peaks are observed for both suspended and supported MoS2, which can be attributed to the thermal expansion of the crystal lattice of MoS2[27,28].
Figure 3. Temperature-dependent Raman spectra of (A) supported and (B) suspended MoS2.
For a more detailed analysis of the difference between suspended and supported MoS2, the Raman spectra presented in Figure 3 were deconvoluted using the Lorentz/Gaussian mixed function. The peak positions of the 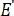and 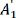modes are plotted as a function of temperature in Figure 4 for comparison. The temperature-dependent evolutions of the frequency shifts for supported and suspended MoS2 samples are similar and vary approximately linearly with increasing temperature. It is well known that mechanically exfoliated MoS2 is transferred and attached on a substrate by weak van der Waals forces. Therefore, the TEC mismatch between MoS2 and the substrate induces biaxial stress into MoS2 as the temperature changes and becomes a prominent factor that modulates the frequency shift of the Raman peaks. The Raman frequency evolutions of suspended MoS2 demonstrate that the substrate effect is exerted on the MoS2 layer as a whole, although the suspended zone of MoS2 is not directly in contact with the substrate.
Figure 4. Frequency shifts of (A) 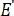and (B) 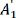modes of suspended and supported MoS2 as a function of temperature. The blue and red lines show the fitting results obtained using a linear equation of temperature.
Moreover, as shown in Figure 4, the temperature evolution of the 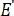mode is significantly different from that of the 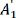mode. For the 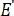mode, the temperature-dependent frequency shift for suspended MoS2 is much closer to that of supported MoS2. In sharp contrast, the temperature-dependent evolutions of the 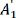mode of suspended MoS2 are very different from those of supported MoS2. The temperature dependences of the 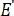and 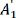modes are fitted using the Grüneisen model[29,30]:
where ω0 is the frequency at 0 K and χ is the temperature coefficient. The temperature coefficients of the 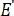mode (
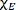) are -0.0985 and -0.0129 cm-1/K for suspended and supported MoS2, respectively. For the 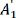mode, the temperature coefficients (
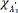) are -0.00952 and -0.00316 cm-1/K for supported and suspended MoS2, respectively. Remarkably, the 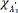of suspended MoS2 is just 34.1% of that of supported MoS2. This suggests that the 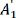mode is more sensitive to the substrate (or dielectric environment). In addition to the TEC mismatch, charge transfer between the TMD film and the substrate or through interfacial states can also influence the temperature evolution of the 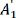peak. Su et al.[31] observed the accelerated redshift of the 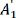mode of MoS2 with increasing temperature, which was attributed to the enhanced charge injection from the substrate into the film and the decomposition of adsorbed contaminants. Through the strong electron-phonon interaction, the electron doping effect leads to frequency shifts of the 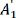mode[32,33]. In contrast, the electron doping effect can be ignored in the temperature-dependent 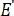mode, which could be used to estimate the thermal strain in monolayer MoS2.
According to the literature, the temperature-dependent Raman frequency shift of freestanding MoS2 can be commonly attributed to the thermal expansion of the lattice [ΔωE(T)] and the anharmonic effect [ΔωA(T)], which changes the phonon self-energy[34]. The intrinsic frequency shift of freestanding MoS2 [Δωint(T)] can be written as:
For the temperature-induced frequency shifts of supported MoS2, both common thermal effects and TEC mismatch-induced strains must be taken into consideration. As a result, the frequency shifts of supported MoS2 can be expressed as[21,34]:
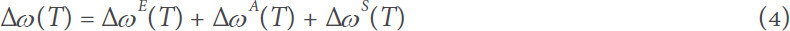
where Δω(T) can be obtained using the frequency position at certain temperature T [ω(T)], shown in Figure 4 subtracted by the peak position at room temperature T0 = 293 K [ω(T0)].
The term ΔωS(T) represents the TEC mismatch-induced frequency shift, which can be expressed as:
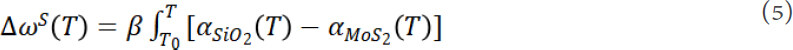
where β is the biaxial strain coefficient of Raman modes 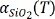and 
and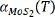 
are the temperature-dependent TECs of SiO2 and MoS2, respectively. The value of β can be taken from the literature[35].
It is known that ΔωE(T) and ΔωA(T) are the intrinsic frequency shifts of MoS2 [Δωint(T)], which are independent of the substrate. For the measured temperature-dependent Raman shifts in this work, the discrepancy in the frequency shifts between suspended and supported MoS2 originates only from the TEC mismatch-induced frequency shift between MoS2 and the substrate. Therefore, after subtracting ΔωS(T), the obtained values for suspended and supported MoS2 should be the same [Δωint(T)]:
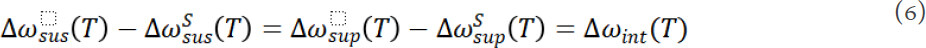
Using Equation (6), the value of 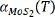can be deduced if we can obtain 
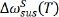and 
However, the TEC mismatch-induced frequency shift 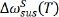for suspended MoS2 is challenging to experimentally determine. Because the MoS2 flake that surrounds the suspended MoS2 zone is still attached to the substrate, the TEC mismatch-induced strain can affect the Raman shift of suspended MoS2 to a certain extent.
Numerical simulations based on finite element theory (FET) provide a route to obtaining the thermal strain in suspended MoS2. For the further study of the distribution of the thermal strain field, thermal strains at different temperatures were solved. In order to solve the FET simulation, the TECs for SiO2 and MoS2 should be provided as material parameters. The 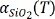is adopted from the literature, whereas 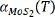is identified in this work. In the first step, we can use the 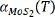previously obtained using first-principles calculation in the simulations[36]. The simulation results are presented in Supplementary Figure 1. It is assumed that the thermal strain is zero in the MoS2 samples at room temperature (T0 = 293 K). In fact, the strain distribution obtained using the FET simulations is composed of two components, namely, the strain due to the thermal expansion of the MoS2 layer and the strain induced by the TEC mismatch between MoS2 and the substrate. In order to obtain the strain induced by the TEC mismatch, FET simulations were also performed on a bare MoS2 flake (see Supplementary Figure 2), which is used to subtract the strain obtained based on the film-substrate model illustrated in Figure 1. The obtained TEC mismatch-induced strains ε(T) for the suspended and supported MoS2 are listed in Table 1. As demonstrated in the literature, the relationship between the TEC-induced strain and Raman shift can be expressed as[35]:
Simulated strain and the corresponding Raman shifts of the 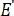mode for suspended and supported MoS2 at selected temperatures
| T (K) | 100 | 200 | 300 | 400 | 500 |
|---|---|---|---|---|---|
| εsus (%) | 0.005434 | 0.004523 | -0.0004271 | -0.007408 | -0.01319 |
| εsup (%) | 0.006833 | 0.005673 | -0.0005339 | -0.009233 | -0.01640 |
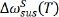| (cm-1) | -0.7227 | -0.6016 | 0.05680 | 0.9853 | 1.755 |
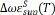 (cm-1) | -0.9088 | -0.7545 | 0.07101 | 1.228 | 2.182 |
Therefore, the thermal strain-induced Raman shift can be obtained using Equation (7). The calculated TEC mismatch-induced strain and corresponding Raman shifts are listed in Supplementary Table 2. By bringing the 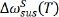and calculated by Equation (7) into Equation (6), it is found that the terms on the left- and right-hand sides cannot be consistent. This implies that the 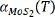reported in previous work is inconsistent with the experimental results in our work. Therefore, in order to meet the requirements for Equation (6), a numerical inversion method was employed to select an optimum TEC of MoS2. A flowchart for the numerical inversion procedure is plotted in Supplementary Figure 3.
With the help of the numerical inversion process, the proper TEC of monolayer MoS2 that satisfies Equation (6) was obtained. Employing the calculated 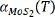, the simulation results for 100, 293 and 500 K are plotted in Figure 5 to illustrate the typical evolution of the strain distribution in the suspended and supported MoS2. As shown in Figure 5A and B, the strain in both two MoS2 samples is zero at room temperature. Figure 5C and D show the strain of SUP-MoS2 and SUS-MoS2 at 100 K, respectively. It can be seen that the thermal strain in SUP-MoS2 caused by the thermal stress is uniform, while the deformation on the SUS-MoS2 mainly occurs on the central circular microhole and gradually decreases in the annular direction with a weak change. From the simulation results, it can be concluded that MoS2 sustains compressive strain. The deformation of SUS-MoS2 is larger because of the binding effect without the substrate. Because the TEC of MoS2 is larger than that of SiO2, MoS2 shrinks faster with decreasing temperature and the deformation of MoS2 is inhibited by SiO2. Therefore, the strain in SUS-MoS2 is larger than that of SUP-MoS2. Figure 5E and F show the strain of SUP-MoS2 and SUS-MoS2 at 500 K. From the simulation results, it can be concluded that MoS2 experiences suppressed tensile strain. Similarly, the SUS-MoS2 deformation is greater due to the absence of the binding force of the substrate.
Figure 5. Numerical simulation results of supported and suspended MoS2: (A), (C), (E) corresponding to the strain of SUP-MoS2 at 293, 100 and 500 K, respectively; (B), (D), (F) corresponding to the strain of SUS-MoS2 at 293, 100 and 500 K, respectively.
Using the same 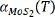that was adopted in Figure 5, FET simulations were also performed on a bare MoS2 flake at different temperatures (see Supplementary Figure 4). By employing the simulated thermal strain in bare MoS2, the TEC mismatch-induced strains for suspended and supported MoS2 were calculated. Then, by employing Equation (7), the frequency shifts of the 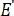mode for suspended and supported MoS2 are calculated and listed in Table 1.
The suitable 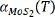obtained by the combination of the numerical simulation and Raman spectroscopy is plotted in Figure 6. One can see that the sign of 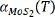is positive in the test temperature range. As shown in Table 2, the value of the 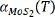obtained in this work is close to the values reported in the literature. Taking the TEC at room temperature for example, the 
obtained in this work is 7.13 (10-5 K-1), while Ding et al.[12] reported an of just 2.44 (10-5 K-1) obtained by DFPT calculation. In contrast, the 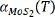obtained in this work is in good agreement with previous results estimated experimentally. Late et al.[29] reported a room-temperature 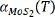of 8.2 (10-5 K-1) obtained by combining temperature-dependent Raman spectroscopy and first-principles calculations. In addition, it is found that the TEC of MoS2 is much larger than that of SiO2. Therefore, MoS2 suppresses a tensile stress from the substrate, whether the sample was cooled or heated.
Figure 6. TEC obtained by combining temperature-dependent Raman spectroscopy and finite element simulations.
Comparison of the TEC of MoS2 obtained from this work and those reported in the literature
Conclusions
In this work, we proposed a feasible method to assess the TEC of monolayer MoS2 by combining micro-Raman spectroscopy and numerical simulations. Suspended and supported MoS2 were systematically investigated using Raman spectroscopy in a temperature range from 77 to 557 K, which exhibited an obvious discrepancy in the evolution of Raman frequency shifts, demonstrating the critical effect due to the TEC mismatch between MoS2 and the substrate. Finite element simulations were used to calculate the TEC mismatch-induced thermal strain and Raman shift in the suspended and supported MoS2. By matching the simulation results to the experimental results, the TEC of MoS2 was determined through a numerical inversion method. This method proposed in our work is a reasonable and adoptable route for determining the TEC of MoS2, which can also be employed to obtain the TEC of 2D materials.
Declarations
Authors’ contributionsDesign, writing review and editing: Yang Y, Long LC
Data analysis: Lin ZT, Li RF
Data acquisition: Liu WG, Li YT, Zhu K
Sample fabrication: Tian SB
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work was supported by the National Key Research and Development Program of China (No. 2018YFB0703500; No.2016YFA0200800), the National Natural Science Foundation of China (No. 11704401; No.12074420; No.11674387; No.61905274), the Key Deployment Project of Centre for Ocean Mega-Research of Science, Chinese academy of science (No. COMS2020J03).
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable
Copyright© The Author(s) 2021.
REFERENCES
1. Chhowalla M, Liu Z, Zhang H. Two-dimensional transition metal dichalcogenide (TMD) nanosheets. Chem Soc Rev 2015;44:2584-6.
2. Lv R, Robinson JA, Schaak RE, et al. Transition metal dichalcogenides and beyond: synthesis, properties, and applications of single- and few-layer nanosheets. Acc Chem Res 2015;3:897.
3. Huang X, Zeng Z, Zhang H. Metal dichalcogenide nanosheets: preparation, properties and applications. Chem Soc Rev 2013;42:1934-46.
4. Chhowalla M, Shin HS, Eda G, Li LJ, Loh KP, Zhang H. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat Chem 2013;5:263-75.
5. Ding Y, Wang Y, Ni J, Shi L, Shi S, Tang W. First principles study of structural, vibrational and electronic properties of graphene-like MX2 (M=Mo, Nb, W, Ta; X=S, Se, Te) monolayers. Physica B Condens Matter 2011;406:2254-60.
6. Mak KF, Lee C, Hone J, Shan J, Heinz TF. Atomically thin MoS2: a new direct-gap semiconductor. Phys Rev Lett 2010;105:136805.
7. Radisavljevic B, Radenovic A, Brivio J, Giacometti V, Kis A. Single-layer MoS2 transistors. Nat Nanotechnol 2011;6:147-50.
8. Yu Y, Yu Y, Xu C, et al. Engineering substrate interactions for high luminescence efficiency of transition-metal dichalcogenide monolayers. Adv Funct Mater 2016;26:4733-9.
9. Dai Z, Liu L, Zhang Z. Strain engineering of 2D materials: issues and opportunities at the interface. Adv Mater 2019;31:e1805417.
10. Yan Z, Liu G, Khan JM, Balandin AA. Graphene quilts for thermal management of high-power GaN transistors. Nat Commun 2012;3:827.
11. Sevik C. Assessment on lattice thermal properties of two-dimensional honeycomb structures: Graphene, h-BN, h-MoS2, and h-MoSe2. Phys Rev B 2014;89.
12. Ding Y, Xiao B. Thermal expansion tensors, Grüneisen parameters and phonon velocities of bulk MT 2 (M = W and Mo; T = S and Se) from first principles calculations. RSC Adv 2015;5:18391-400.
13. Huang LF, Gong PL, Zeng Z. Correlation between structure, phonon spectra, thermal expansion, and thermomechanics of single-layer MoS2. Phys Rev B 2014;90.
14. Yuan J, Lv Z, Lu Q, Cheng Y, Chen X, Cai L. First-principles study of the phonon vibrational spectra and thermal properties of hexagonal MoS2. Solid State Sciences 2015;40:1-6.
15. Liang L, Zhang J, Sumpter BG, Tan QH, Tan PH, Meunier V. Low-frequency shear and layer-breathing modes in Raman scattering of two-dimensional materials. ACS Nano 2017;11:11777-802.
16. Wang Y, Cong C, Qiu C, Yu T. Raman spectroscopy study of lattice vibration and crystallographic orientation of monolayer MoS2 under uniaxial strain. Small 2013;9:2857-61.
17. Saigal N, Wielert I, Čapeta D, et al. Effect of lithium doping on the optical properties of monolayer MoS2. Appl Phys Lett 2018;112:121902.
18. Huang X, Zhang L, Liu L, et al. Raman spectra evidence for the covalent-like quasi-bonding between exfoliated MoS2 and Au films. Sci China Inf Sci 2021;64.
19. Mouri S, Matsuda K, Nanishi Y, Araki T. Thermal conductivity of van der Waals hetero-bilayer of MoS2/MoSe2. Appl Phys Express 2020;13:075001.
20. Zhang L, Lu Z, Song Y, et al. Thermal expansion coefficient of monolayer molybdenum disulfide using micro-raman spectroscopy. Nano Lett 2019;19:4745-51.
21. Lin Z, Liu W, Tian S, Zhu K, Huang Y, Yang Y. Thermal expansion coefficient of few-layer MoS2 studied by temperature-dependent Raman spectroscopy. Sci Rep 2021;11:7037.
22. Huang Y, Pan YH, Yang R, et al. Universal mechanical exfoliation of large-area 2D crystals. Nat Commun 2020;11:2453.
23. Baek SH, Choi Y, Choi W. Large-area growth of uniform single-layer MoS2 thin films by chemical vapor deposition. Nanoscale Res Lett 2015;10:388.
24. Yang Y, Liu W, Lin Z, et al. Micro-defects in monolayer MoS2 studied by low-temperature magneto-Raman mapping. J Phys Chem C 2020;124:17418-22.
25. Chakraborty B, Matte HSSR, Sood AK, Rao CNR. Layer-dependent resonant Raman scattering of a few layer MoS2: Raman scattering of a few layer MoS2. J Raman Spectrosc 2013;44:92-6.
26. Tian S, Yang Y, Liu Z, et al. Temperature-dependent Raman investigation on suspended graphene: Contribution from thermal expansion coefficient mismatch between graphene and substrate. Carbon 2016;104:27-32.
27. Huang X, Gao Y, Yang T, Ren W, Cheng HM, Lai T. Quantitative analysis of temperature dependence of raman shift of monolayer WS2. Sci Rep 2016;6:32236.
28. Chen Y, Wen W, Zhu Y, et al. Temperature-dependent photoluminescence emission and Raman scattering from Mo1-x W x S2 monolayers. Nanotechnology 2016;27:445705.
29. Late DJ, Shirodkar SN, Waghmare UV, Dravid VP, Rao CN. Thermal expansion, anharmonicity and temperature-dependent Raman spectra of single- and few-layer MoSe2 and WSe2. Chemphyschem 2014;15:1592-8.
30. Zouboulis ES, Grimsditch M. Raman scattering in diamond up to 1900 K. Phys Rev B Condens Matter 1991;43:12490-3.
31. Su L, Yu Y, Cao L, Zhang Y.
32. Chakraborty B, Bera A, Muthu DVS, Bhowmick S, Waghmare UV, Sood AK. Symmetry-dependent phonon renormalization in monolayer MoS2 transistor. Phys Rev B 2012;85.
33. Iqbal MW, Shahzad K, Akbar R, Hussain G. A review on Raman finger prints of doping and strain effect in TMDCs. Microelectron Eng 2020;219:111152.
34. Yoon D, Son YW, Cheong H. Negative thermal expansion coefficient of graphene measured by Raman spectroscopy. Nano Lett 2011;11:3227-31.
35. McCreary A, Ghosh R, Amani M, et al. Effects of uniaxial and biaxial strain on few-layered terrace structures of MoS2 grown by vapor transport. ACS Nano 2016;10:3186-97.
36. Zhang H, Wu Y. Electronic, thermal expanding, and optical absorption properties of transition metal dichalcogenides: a first-principles study. J Wuhan Univ Technol-Mat Sci Edit 2018;33:1355-9.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Yang Y, Lin Z, Li R, Li Y, Liu W, Tian S, Zhu K, Long L. Thermal expansion coefficient of monolayer MoS2 determined using temperature-dependent Raman spectroscopy combined with finite element simulations. Microstructures 2021;1:2021002. http://dx.doi.org/10.20517/microstructures.2021.02
AMA Style
Yang Y, Lin Z, Li R, Li Y, Liu W, Tian S, Zhu K, Long L. Thermal expansion coefficient of monolayer MoS2 determined using temperature-dependent Raman spectroscopy combined with finite element simulations. Microstructures. 2021; 1(1): 2021002. http://dx.doi.org/10.20517/microstructures.2021.02
Chicago/Turabian Style
Yang, Yang, Zhongtao Lin, Renfei Li, Yutong Li, Wuguo Liu, Shibing Tian, Ke Zhu, Lianchun Long. 2021. "Thermal expansion coefficient of monolayer MoS2 determined using temperature-dependent Raman spectroscopy combined with finite element simulations" Microstructures. 1, no.1: 2021002. http://dx.doi.org/10.20517/microstructures.2021.02
ACS Style
Yang, Y.; Lin Z.; Li R.; Li Y.; Liu W.; Tian S.; Zhu K.; Long L. Thermal expansion coefficient of monolayer MoS2 determined using temperature-dependent Raman spectroscopy combined with finite element simulations. Microstructures. 2021, 1, 2021002. http://dx.doi.org/10.20517/microstructures.2021.02
About This Article
Copyright
Data & Comments
Data
Cite This Article 4 clicks
Like This Article 1
likes
Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.