Design of super-elastic freestanding ferroelectric thin films guided by phase-field simulations
Abstract
Understanding the dynamic behavior of domain structures is critical to the design and application of super-elastic freestanding ferroelectric thin films. Phase-field simulations represent a powerful tool for observing, exploring and revealing the domain-switching behavior and phase transitions in ferroelectric materials at the mesoscopic scale. This review summarizes the recent theoretical progress regarding phase-field methods in freestanding ferroelectric thin films and novel buckling-induced wrinkled and helical structures. Furthermore, the strong coupling relationship between strain and ferroelectric polarization in super-elastic ferroelectric nanostructures is confirmed and discussed, resulting in new design strategies for the strain engineering of freestanding ferroelectric thin film systems. Finally, to further promote the innovative development and application of freestanding ferroelectric thin film systems, this review provides a summary and outlook on the theoretical modeling of freestanding ferroelectric thin films.
Keywords
INTRODUCTION
The advancement of semiconductor materials and micro-/nanofabrication technologies has promoted the growth of the modern electronics industry. Various materials with excellent qualities which meet the needs of the automated and intelligent manufacturing industries have been designed and prepared gradually. In recent decades, silicon-based complementary metal-oxide-semiconductor (CMOS)-centric design procedures have played a critical role in the modern electronics industry. However, the emergence of flexible electronic devices has presented new challenges for the traditional CMOS processing technique and new opportunities for the existing electronic manufacturing industry[1-3]. Flexible electronic materials can be applied to fabricate flexible displays[4-6], nanosensors[7-9], health monitors[10-12] and other electronic devices for intelligent processing and human-computer interactions[13]. For example, flexible electronic materials can integrate cutting-edge technologies, including intelligent signal processing, real-time information sensing and nanogenerators, to improve the intelligence level of biocompatible electronics. As a result, they play an increasingly critical role in the intelligent monitoring of human health and biomedical applications, which will significantly change the future of healthcare and the relationship between patients and electronics. Furthermore, with the rise and combination of artificial intelligence and the Internet of Things (AI and IoT, i.e., AIoT), these electronic devices have an increasingly wide range of applications.
However, most traditional inorganic materials with excellent electronic properties show poor stability in complex stress environments, thereby severely limiting their application prospects in flexible electronic devices. Therefore, finding and preparing basic materials with excellent electronic and flexible properties is one of the keys to developing the flexible electronics industry. Generally, two complementary approaches can be applied to obtain electronic materials with superior mechanical and electrical properties. The first is the design and innovation of flexible materials by developing novel materials, including polymers[14,15], hydrogels[16,17], liquid metals[18,19] and freestanding films[20,21]. The second is structural optimization design by designing traditional high-performance electronic materials into appropriate mechanical structures[22,23], including wrinkled[24,25], origami[26,27], kirigami[28,29] and textile[30,31] structures.
Ferroelectric perovskite oxides are indispensable materials in the modern electronics industry because of their abundance of excellent physical properties, extensive research value and long-term practical application prospects. High-performance ferroelectric oxides are critical components in the current electronics industry because they have outstanding electrical properties, including ferroelectricity, piezoelectricity, pyroelectricity and dielectricity. They are widely applied in high-efficiency memories[32-35], microsensors[36,37], high-frequency filters[38,39], energy harvesting systems[40,41], high-energy-density capacitors[42-45], ultrasonic medical treatment[46,47] and other related devices[48-51], and are also expected to be applied in the field of high-temperature superconductivity[52,53]. However, perovskite ferroelectrics are generally considered to be brittle and unbendable[54,55]. Therefore, if they can be transformed into flexible structures through the above two approaches, it will significantly accelerate the growth of the flexible electronics industry and occupy increasingly widespread applications. In addition, organic ferroelectric polymer materials[56-60], such as poly(vinylidene fluoride) and its copolymers, have excellent properties and can achieve sizeable mechanical deformation, such as stretching, bending and twisting, without being damaged. Therefore, for the design and processing of flexible electronic materials, ferroelectric materials with flexibility and super-elasticity have received extensive attention due to their excellent mechanical and electrical properties.
This review mainly focuses on super-elastic freestanding ferroelectric thin films. First, current super-elastic freestanding ferroelectric films and their experimental characterization results are summarized. Subsequently, the origin of the super-elasticity of freestanding ferroelectric thin films is revealed and explained on the basis of phase-field simulations. The designed mechanical structures based on super-elastic ferroelectric thin films, such as two-dimensional (2D) wrinkles and three-dimensional (3D) nanosprings, are then introduced [Figure 1]. Finally, the outlook and prospects for super-elastic flexible freestanding ferroelectric thin films are presented.
Figure 1. Novel mechanical structures and applications of super-elastic/flexible freestanding ferroelectric thin films. Novel mechanical structures include 2D bending (Left : reprinted with permission[61]. Copyright 2019, The American Association for the Advancement of Science. Right: reprinted with permission[62]. Copyright 2020, AIP Publishing), 2D zigzag-wrinkling (Top: reprinted with permission[63]. Copyright 2020, Wiley-VCH. Bottom: reprinted with permission[64].Copyright 2022, American Chemical Society), 2D toroidal-wrinkling (reprinted with permission[65]. Copyright 2021, The American Association for the Advancement of Science), and 3D twisting (reprinted with permission[66]. Copyright 2022, Wiley-VCH) structures. Flexible applications include non-volatile memories (reprinted with permission[67]. Copyright 2013, Wiley-VCH), flexible displays (reprinted with permission[68]. Copyright 2004, Elsevier), nano-sensors (reprinted with permission[69]. 2018, CC BY license), health monitors (reprinted with permission[70]. Copyright 2016, Wiley-VCH), nano-generators (reprinted with permission[71]. Copyright 2020, American Chemical Society), and energy harvesters (reprinted with permission[72]. 2016, CC BY license).
SUPER-ELASTIC FREESTANDING FERROELECTRIC FILMS
Preparation of flexible ferroelectric thin films
Due to the clamping effect of the rigid substrates during the traditional process of preparing ferroelectric thin films, they often show far poorer electrical performance, in terms of piezoelectric constant, switching speed and switching voltage[73-76], than those of freestanding materials. With the rapid development of new fabrication techniques for thin films[77], high-quality flexible freestanding ferroelectric thin films with excellent mechanical elastic and electrical properties[78,79] can be fabricated. Since many excellent reviews[21,80-83] have discussed the preparation of flexible freestanding ferroelectric films, we only briefly summarize the methods for obtaining them here.
Direct growth. Ferroelectric thin films can be directly grown on flexible substrates, including metals (such as foils), organic polymers (such as polyimide (PI)) and 2D layered materials (such as mica and graphene). Metal foils have low brittleness, excellent electrical conductivity and outstanding thermal stability as flexible substrates. Due to the unfavorable thermal expansion mismatch and ion diffusion between the ferroelectric thin film and the metal foil, a buffer layer is usually grown on the surface of the substrate to solve these problems. For instance, Won et al. used LaNiO3, which has closely matched lattice parameters (~0.38 nm) with most perovskite ferroelectric materials, as a conductive buffer layer and the prepared Pb(Zr,Ti)O3 films exhibited superior ferroelectricity and piezoelectricity than those on conventional Pt/Ti/SiO2/Si substrates[84]. Although PI substrates have better mechanical ductility and flexibility, the temperature they can withstand (< 400 °C) cannot reach the crystallization temperature of ferroelectric oxides (> 600 °C). Bretos et al. proposed a series of solution-based approaches to realize the low-temperature crystallization of ferroelectric thin films, such as BiFeO3 and Pb(Zr,Ti)O3[85-89]. In addition to the aforementioned direct growth on flexible substrates, mechanical exfoliation along heterointerfaces after the deposition of ferroelectric thin films onto 2D layered materials has also been developed. Through van der Waals epitaxy, weak bonds are formed between the thin film and the 2D layered substrate, providing an opportunity for mechanical exfoliation to obtain freestanding ferroelectric thin films with minimal internal stress. Mica[90-92] and graphene[93,94] are promising 2D layered materials as flexible substrates with atomic-level surface roughness, good stability and mechanical flexibility. High-quality flexible ferroelectric films with good mechanical integrity can be grown on mica and graphene substrates by van der Waals epitaxy, demonstrating their potential for next-generation electronics.
Laser lift-off process. The laser lift-off method was initially proposed and developed for transferring epitaxial GaN films from substrates[95,96] and was later utilized to prepare and obtain flexible freestanding ferroelectric oxide films. The specific process is to first deposit a ferroelectric oxide film (such as via a sol-gel method) on a wide band gap substrate (such as sapphire). A laser then irradiates the sample from the back of the substrate to partially vaporize the interface between the ferroelectric film and the substrate. Finally, a freestanding ferroelectric oxide film is obtained. However, this stripping method ablates the ferroelectric thin film, forming a thermally damaged layer at the interface of the thin film, so it is necessary to introduce a sacrificial layer[97,98] and further anneal to recover the surface structure[99].
Wet etching. Obtaining freestanding ferroelectric thin films by wet etching is a promising approach with significant advantages. According to the parts to be etched, wet etching can be divided into wet etching of the substrate, wet etching of the interface layer between the thin film and substrate and wet etching of the sacrificial layer, with the latter being the more cost-effective method[99]. Single-crystal ferroelectric thin films have been grown on sacrificial buffer layer (e.g., La0.7Sr0.3MnO3[100,101], Sr3Al2O6[102-106] and BaO[107])-coated SrTiO3 (STO) substrates. Subsequently, the sacrificial buffer layer is dissolved by selective etching to release the freestanding ferroelectric oxide film. Finally, the freestanding thin films can be transferred to flexible substrates, such as polyethylene terephthalate[75,108] or polydimethylsiloxane (PDMS)[61,105,109-111]. They can also be transferred to silicon (Si) substrates and combined with Si-based electronics. For example, Han et al. selected water-soluble Sr3Al2O6 as the sacrificial layer to grow a series of (PbTiO3)m/(SrTiO3)n bilayers on STO substrates. After the Sr3Al2O6 sacrificial layer was dissolved, the bilayer films were laminated on a platinized Si (001) substrate[112]. Exotic skyrmion-like polar nanodomains are observed in bilayer films, which provide a new strategy for integration into Si-based high-density storage technologies.
Super-elastic behavior of freestanding single-crystal ferroelectric thin films
Ferroelectric oxides are generally considered to be brittle and non-bendable because of their grain boundaries and the small ductility of ionic or covalent bonds within the crystal. In addition, the low fracture toughness (in the order of 1 MPa·m1/2)[55] means that ferroelectric oxides are prone to fracture. Nevertheless, the high-quality freestanding single-crystal ferroelectric thin films obtained by the above freestanding methods have attractive mechanical flexibility and super-elasticity. Dong et al. fabricated freestanding single-crystal BaTiO3 (BTO)[61] and BiFeO3 (BFO)[110] ferroelectric thin films by pulsed-laser deposition (PLD) when using Sr3Al2O6 as a sacrificial layer that was dissolved in water. As shown in Figure 2A and B, the fabricated BTO films could undergo a ~180° folding without any cracks in in-situ scanning electron microscopy (SEM) bending tests and also recover to their original shape after removing the bending load. This behavior demonstrates their super-elasticity and flexibility. Similarly, the BFO film could withstand cyclic folding tests of up to 180° and the largest bending strain was observed to reach 5.42% during the bending process. Furthermore, freestanding flexible multiferroic BiMnO3 films were synthesized by
Figure 2. (A) In situ SEM image of the BTO film folded to about 180°. (B) SEM images of bending and recovery process of a BTO film. (C) The c/a ratio of freestanding PTO films as a function of uniaxial strain. The inset is schematics of as-grown and stretched polarization state. (D) Electromechanical coupling responses of freestanding BTO films folded and unfolded under an electron beam-induced field. (E) Open circuit voltage (Voc) and short circuit current density (Jsc) of freestanding BFO device as a function of strain gradient. (F) The bending-expansion and bending-shrinkage effects were observed in upward and downward bent BFO films. Panels A and B reprinted with permission[61]. Copyright 2019, The American Association for the Advancement of Science. Panel C reprinted with permission[106]. Copyright 2020, Wiley-VCH. Panel D reprinted with permission[113]. Copyright 2020, American Chemical Society. Panel E reprinted with permission[109], 2020, CC BY license. Panel F reprinted with permission[114], 2022, CC BY license.
Freestanding thin films, in contrast to epitaxial thin films, are free from the clamp of the substrate and therefore provide ideal and unique flexible platforms for continuously controllable strain engineering. For example, Han et al. applied a continuous uniaxial tensile strain as high as 6.4% to freestanding PbTiO3 (PTO) films, far exceeding the realizable value for epitaxial PTO films [Figure 2C][106]. This demonstrates the efficient and meaningful strain tunability of freestanding ferroelectric films, which deserves further exploration and design. Flexible freestanding oxides also provide a new direction for exploring outstanding performance, including piezoelectricity and flexoelectricity. By PLD, Elangovan et al. fabricated 30-nm-thick flexible freestanding piezoelectric BTO thin films with good electromechanical-coupling properties[113]. As shown in Figure 2D, under an external electric field, the thin film could fold gradually and continuously by 180° and the fold-unfold cycles were reversible. The contribution of the flexoelectric effect caused by the strain gradient induced by bending in flexible films is considerable. Guo et al. demonstrated the tunable photovoltaic effect in freestanding single-crystal BFO films and obtained multilevel photoconductance in BFO by altering the bending radius of the flexible device [Figure 2E][109]. As shown in Figure 2F, Cai et al. observed a giant flexoelectric response at strain gradients of up to ~3.5 × 107 m-1 in a wrinkled structure based on high-quality flexible freestanding BFO perovskite oxides[105,114]. Furthermore, the unusual bending expansion and shrinkage observed in bent freestanding BFO are also never seen in crystalline materials. Corresponding theoretical models show that these novel phenomena are attributed to the combined action of flexoelectricity and piezoelectricity. These experimental observations and theoretical models may provide a new path toward the strain and strain-gradient engineering of super-elastic freestanding ferroelectric thin films.
PHASE-FIELD METHOD OF FERROELECTRICS
The mechanical, electrical, optical, magnetic and other macroscopic physical properties of a material are not only related to its chemical composition but also largely depend on the characteristics of its internal microstructure. Such microstructures can be phase structures composed of crystalline structures, grains with different orientations, ferroelectric domains and dislocations, which are usually at the mesoscopic scale, ranging from nanometers to micrometers[115]. In material processing and service, external stimuli may cause the microstructure to move away from equilibrium. Furthermore, the corresponding theoretical description requires a combination of non-equilibrium thermodynamics and kinetic theories. Thermodynamic theory and kinetic principles determine the evolution direction and path of the microstructure, respectively. Due to the complexity and nonlinearity of microstructural evolution, we usually use numerical simulation methods to predict the evolution process. Compared to traditional modeling methods involving the explicit tracking of interface locations, the phase-field method has become one of the most powerful methods for simulating the evolution process of various microstructures. The phase-field method is based on the Landau theory of phase transitions, which holds that one of the standard features of a phase transition is a change in the symmetry of a system. Changes in symmetry imply changes in the degree of order, which can be measured by the order parameter (as a space function). According to the selection of order parameters, ferroelectrics are classified as proper or improper. For BTO, PTO and other proper ferroelectrics, the selected order parameter is the ferroelectric polarization P that can explain the symmetry change in the phase transition. However, for improper ferroelectrics, such as hexagonal manganites h-REMnO3 (RE = rare earth), the primary order parameter is the amplitude Q and phase Φ characterizing the structural trimerization and the secondary order parameter is the polarization P induced by the trimerization[116,117].
Theoretical fundamentals of phase-field method
The phase-field method with diffusive interfaces considers the non-local energy of the polarization gradient, which is different from the homogeneous assumption in thermodynamic models. By solving the phase-field equations, the order parameters in the space and time distribution can be calculated, the spatially continuous but inhomogeneous polarization distribution in the ferroelectric at different times can be determined and the evolution process of the microstructure can be obtained. The evolution process is a direct consequence of the minimization of the total free energy of the entire system, where ferroelectric polarization switching and phase transitions can be simulated by solving the time-dependent Ginzburg-Landau equation[118-122]:
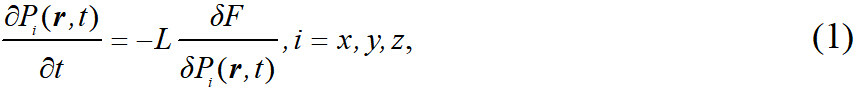
where Pi(r,t) is the spontaneous polarization, r is the spatial coordinate, t is the evolution time, L is the kinetic coefficient that is related to the domain evolution and F is the total free energy that includes the contributions from the Landau, gradient, elastic, electric and flexoelectric coupling energies:
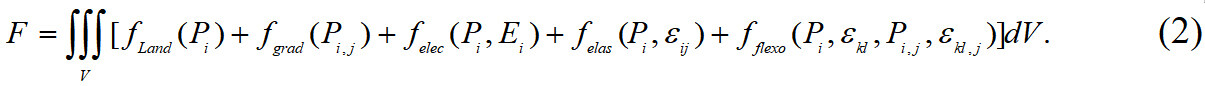
The Landau energy density fLand and the gradient energy density fgrad are given by:
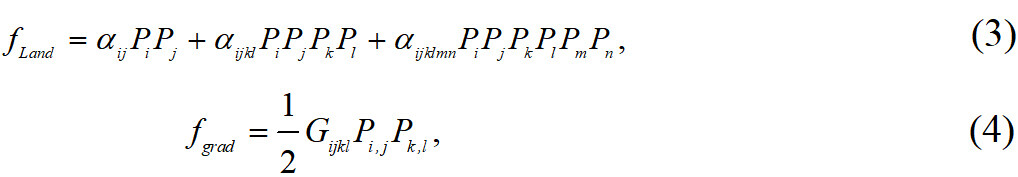
where αij, αijkl and αijklmn are the Landau coefficients, Gijkl is the gradient energy coefficient and Pi,j= ∂Pi/∂xj.
The electric energy density felec is expressed as:

where Ei is the electric field component, ε0 is the vacuum permittivity and κij is the dielectric constant. The electrical quantities should satisfy the electrostatic equilibrium (Poisson’s) equation:

where φ is the electric potential and ρ represents the total space charges. The electric field is related to the potential through Ei = -φ,i.
The elastic energy density felas and the flexoelectric coupling energy density fflexo can be written as:
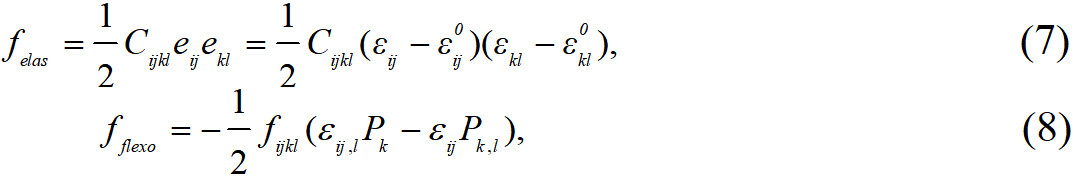
where Cijkl is the elastic stiffness tensor, eij is the elastic strain and εij and
The mechanical quantities are satisfied by solving the mechanical equilibrium equation:

where σij is the stress tensor and bi is the external force per unit volume.
Phase-field model of freestanding ferroelectric thin films
The phase-field model of a freestanding ferroelectric thin film differs from that of an epitaxial ferroelectric thin film with a substrate. As shown in Figure 3A and B, the lattice points of traditional epitaxial ferroelectric thin film models are subjected to compressive (or tensile) misfit strains induced by the substrate. The lattice points in the new phase-field model of the freestanding ferroelectric thin film have deformability characteristics, which can change the volume and shape following the bending deformation of the thin film.
Figure 3. (A) Phase-field model of the epitaxial ferroelectric thin film with a substrate. The dashed box is a schematic of the model lattice under compressive misfit strain. (B) Phase-field model of the bent freestanding ferroelectric thin film. The dashed box is a schematic of the deformable model lattice under bending strain, and the purple line represents the neutral layer of the model. (C) The structural schematic of the phase-field method for freestanding ferroelectric thin films.
The deformation of freestanding ferroelectric films can be set by applying displacement or stress (strain) boundary conditions. For instance, Guo et al. achieved the bending deformation of a freestanding film by applying displacement boundary conditions, explicitly adjusting the rotational inclination of the left and right end of the film along the neutral surface[62]. Moreover, Peng et al. stabilized the film to a bending state by applying stress (strain) boundary conditions, explicitly introducing a bending strain state that exhibits a gradient distribution along the film thickness[110,123,124]. In addition, the top and bottom layers of the film are set as stress-free boundaries to satisfy the freestanding boundary conditions. Therefore, as shown in Figure 3C, for the phase-field method of freestanding ferroelectric thin films, by using the well-established phase-field model of deformable lattices, considering the freestanding boundary conditions and the complex strain (and strain gradient) states caused by the deformation of novel mechanical structures, the nanodomains corresponding to the freestanding ferroelectric structure can be obtained. The mechano-electric coupling relationship and electrical properties (including piezoelectricity and electrocaloric performance) of the freestanding ferroelectric system can then be explored.
MODEL-GUIDED UNDERSTANDING OF SUPER-ELASTICITY IN FREESTANDING FERROELECTRIC THIN FILMS
Freestanding thin films demonstrate the advantages of tunable strain states compared with epitaxial growth on lattice-mismatched substrates. The source of the superior super-elasticity of freestanding films needs to be further explored because it is crucial for their further application in flexible electronics. The super-elasticity of freestanding ferroelectric membranes may originate from the mesoscale ferroelectric domain evolution in the presence of the external deformation. However, the direct observation of the domain structure evolution of nanoscale freestanding films during continuous deformation is challenging by current experimental methods.
The phase-field method can simulate the dynamic evolution of freestanding ferroelectric films during mechanical deformation under external loads and the ferroelectric phase transition behavior under various strains and temperatures. Unlike the domain structure of ferroelectric films under a single strain in previous studies, more complex nanodomains appear due to the coexistence of tensile and compressive strains in bent freestanding films. For instance, Guo et al. and Peng et al. performed phase-field simulations on the bending deformation process of freestanding ferroelectric films to reveal the theoretical origin of the super-elasticity of freestanding ferroelectric films from the perspective of domain evolution[62,123]. During the continuous bending process of a freestanding BTO film, the mixed tensile and compressive stress generated by the bending [Figure 4A] caused the electric dipole to rotate continuously in the transition region, thereby connecting the a and c domains to form “vortex-like” domain structures [Figure 4B]. The formation of “vortex-like” domains essentially eliminates the sharp stress caused by lattice mismatch, allowing the freestanding film to maintain mechanical integrity during the bending process. The continuous rotation of the electric dipole can be explained by the phenomenological Landau theory[61]. As seen from Figure 4C, four minima in the energy landscape exist in a bulk stress-free state of BTO, corresponding to two a domains and two c domains. When in the bending state, the energy barrier between the a and c domains decreases, indicating that the polarization transition between the a and c domains becomes easier. The appearance of “vortex-like” domains has apparent size effects and the a/c phase with a vortex-like structure emerges when the film thickness reaches 12 nm [Figure 4D]. This may indicate that the super-elasticity of freestanding ferroelectric films has a specific relationship with the film thickness.
Figure 4. (A) Strain distribution of n-shape bent freestanding films. (B) Domain structures and surface strain of freestanding BTO thin film at different bending angles. (C) Schematic illustration of free energy landscape of bulk BTO (top) and freestanding thin films upon bending (bottom). (D) Size effect on domain patterns of BTO thin film under bending. (E) Dynamic evolution of ferroelectric domains in freestanding BFO thin films during bending. (F) Dynamic evolution of volume average energy density of freestanding BFO thin films under θ = 17.19° with time step. Panels A, B and D reprinted with permission. Copyright 2020, AIP Publishing[62]. Panel C reprinted with permission. Copyright 2019, American Association for the Advancement of Science[61]. Panels E and F reprinted with permission. Copyright 2021, Elsevier[123].
From the perspective of phase-field energy minimization, the generation of a local ferroelectric vortex and the ferroelectric polarization rotation can effectively promote the reduction in elastic energy and modulate the mechanical stress on the freestanding ferroelectric film during bending, which contributes to the accommodation of the large deformation and super-elasticity. As shown in Figure 4E, Peng et al. investigated the dynamic domain evolution process of bent freestanding BFO films, with an exotic ferroelectric vortex generated by local ferroelastic switching when the bending angle was higher than the critical value (e.g., 17.19° for a thickness of 80 nm)[123]. By comparing the dynamic evolution of different energy densities during the phase-field simulation [Figure 4F], the intrinsic energy barrier
FUNCTIONAL MECHANICAL STRUCTURES BASED ON SUPER-ELASTIC FERROELECTRIC THIN FILMS
Freestanding ferroelectric thin films are ideal for studying the distortion of crystal structures and future applications of ferroelectric materials. Taking flexible carriers for memory logic devices as an example,
Figure 5. (A) Schematic illustration of a ferroelectric nanofilm with rectangular memory units (upper left), a single basic memory unit (upper right), and a bent single memory unit (bottom). (B) Phase diagram of the domain pattern in memory units under bending. All panels reprinted with permission[125], 2014, CC BY license.
2D wrinkled structure of freestanding ferroelectric thin films
The buckling instability mode, which leads to out-of-plane deformation, is prone to occur in thin film structures under certain environmental stimuli (e.g., mechanical forces[126-130], temperature[131], van der Waals interactions[132] and localized diffusion of the solvent[133,134]). For example, when the film is subjected to in-plane compressive stress, it is in an unstable state with high energy. As a result, the film and substrate deform to release compressive stress, thereby reducing the energy of the system. Moreover, because the film thickness h is small, its bending rigidity D = Ef h3/12 is minimal compared to Young’s modulus Ef. Films generally deform via out-of-plane wrinkling to release internal compressive stress by generating bending energy. For the simplest sinusoidal wrinkling mode w(x,y) = Acos(kx), both the wavelength and amplitude are related to the mechanical quantities of the film-substrate system[135-139]:

where Ef and Es are Young’s modulus of the film and substrate, respectively, v is the Poisson’s ratio and λ and A are the wavelength and amplitude of the wrinkle, respectively [Figure 6A].
Figure 6. (A) A thin film on a compliant substrate undergoes surface wrinkling. (B) Schematic of the total energy of the thin film system as a function of the wrinkle amplitude A at small (left) and large (right) film strains (reprinted with permission[137]. Copyright 2005, Elsevier).
The buckling instability of wrinkles is a fascinating nonlinear mechanical model and is very effective in understanding their formation mechanism from an energy perspective. For a film bonded to a compliant substrate, Huang et al. obtained the wavelength and amplitude of the wrinkles for substrates with different moduli and thicknesses by minimizing the energy[137]. As shown in Figure 6B, when the strain of the film εfilm is less than εc, the system minimizes at the state A = 0, and when the strain of the film εfilm exceeds εc, the system wrinkles to an equilibrium amplitude Aeq. The occurrence of buckling modes may lead to structural and functional failure of the membranes, potentially limiting the performance of materials and is often considered to be avoided. In contrast, stress-driven buckling instability can self-assemble ordered surface topographies, including sinusoidal, zigzag, labyrinthine, triangular and checkerboard patterns. The physical properties of wrinkles show broad application prospects in the design of flexible electronic devices, the assembly of 3D complex microstructures[140], the morphological control of innovative optoelectronics and integrated systems[141-143], the measurement of mechanical properties of materials[144,145] and even medical assistance in diagnosis and treatment[146].
The formation of various wrinkled structures has been reported in thin film systems such as metals[126], graphene[132], organics[130,131,133,134], gels[147], biological tissues[148] and more recently in freestanding ferroelectric thin film systems. As shown in Figure 7A, Dong et al. successfully fabricated periodic wrinkle-patterned BTO/PDMS membranes based on an as-prepared super-elastic single-crystal freestanding BTO film[63,64]. Moreover, finely controlled wrinkle patterns, such as sinusoidal, zigzag and labyrinthine patterns, were obtained by changing the anisotropy and magnitude of the applied stress or adjusting the interfacial adhesion conditions. It is noteworthy that the thickness of the super-elastic BTO film significantly affected the period of the wrinkle pattern. The thicker the BTO film, the larger the wavelength, which also conforms to Equation (10), i.e., the wavelength and period of the wrinkle pattern are proportional to the thickness of the film.
Figure 7. (A) Optical microscopy images of wrinkled BTO. The scale bar is 20 µm. (B) Piezoresponse force microscopy (PFM) phase color images of zigzag-wrinkled BTO under scanning force induced by the SPM tip. (C) Distribution of corresponding strain component εxx of zigzag-wrinkled BTO by the SPM tip from phase-field simulations considering the flexoelectric effect. (D) Distribution of “braided-like” polarization of zigzag-wrinkled BTO by the SPM tip. The color bar represents the polarization component Px. (E) IP-PFM phase image showing the toroidal polar topology of wrinkled P(VDF-TrFE) film. (F and G) The in-plane strain and domain structure of the wrinkled P(VDF-TrFE) under an applied tensile strain of 7.3% from phase-field simulations, respectively. (H) The electric toroidal moments corresponding to the domain structure in (G) illustrate the presence of in-plane topological domains. Panel A reprinted with permission[63]. Copyright 2020, Wiley-VCH. Panels B-D reprinted with permission[64]. Copyright 2022, American Chemical Society. Panels E-H reprinted with permission[65]. Copyright 2021, The American Association for the Advancement of Science.
Due to the peculiar morphology of wrinkled ferroelectric films, the strain state is different from the interfacial mismatch strain of conventional epitaxial films. Therefore, a unique ferroelectric domain structure distribution can be generated by applying external loads. For example, the strain field is introduced by a scanning probe, which is quite different from applying out-of-plane strain directly to the epitaxial film, as shown in Figure 7C. Zhou et al. found a periodic “braided” in-plane domain superstructure and opposite out-of-plane domains between peaks and valleys through the modulation of scanning probe microscopy (SPM) tip-induced loading forces, as seen in Figure 7B[64]. This unique domain depends on the strain state induced by the zigzag wrinkle morphology and the loading of the SPM tip. Due to the periodic “braided-like” strain state, the polarization is deflected to the direction parallel (perpendicular) to the tensile strain (compressive strain) εxx, resulting in the formation of the ferroelectric nanodomain structure, as shown in Figure 7D. In addition, some novel wrinkle structures also exist in flexible ferroelectric polymer systems. As shown in Figure 7E, Guo et al. found a periodic toroidal “target-like” wrinkle morphology in a flexible ferroelectric polymer poly(vinylidene fluoride-ran-trifluoroethylene) [P(VDF-TrFE)], as well as a peculiar toroidal topological texture using in-plane piezoresponse force microscopy (IP-PFM) measurements[65]. The distribution of the toroidal domain structure [Figure 7G] is caused by the strain state induced by the “target-like” wrinkle morphology under external tensile strain, which is a periodically alternating tensile and compressive strain [Figure 7F]. According to this calculation, the electric toroidal moment[149] Gz is much larger than Gxand Gy, indicating the existence of in-plane toroidal order [Figure 7H]. Therefore, the morphology of freestanding ferroelectric wrinkled films can be developed as a degree of freedom for strain tuning the domains and physical properties of flexible ferroelectric systems.
3D nanospring structure of freestanding ferroelectric thin films
Ferroelectric materials display a range of individual polar topological states, including flux-closure domains[150,151], vortices[152-155], skyrmion bubbles[156,112,157], merons[158], center domains[159] and sixfold vortex networks[160], as a result of geometrical constraints between structural shape and material interface at the micro/nanoscale. The competition and coupling of elastic, electrostatic and gradient energies can lead to the induction of novel polar topologies that are not stable in conventional bulk ferroelectrics under the combined influence of a sharply increased depolarization field caused by size, noticeable interface and boundary constraint effects. With the demand for the miniaturization and multi-functionalization of functional ferroelectric devices, an increasing number of nanostructures with novel topological ferroelectric domains can be realized through top-down and bottom-up nanofabrication techniques. For example, Shimada et al. designed and studied 2D PTO nanostructures (including honeycomb, kagome and star shapes) by establishing a phase-field model based on a 2D Archimedes lattice[161]. Furthermore, the polarization was gradually rotated at the junctions of different repeating units in these nano-metamaterials to form a continuous flow pattern.
Among the unique nanostructures designed and produced, the emergence of nanosprings has received considerable attention. Nanosprings can achieve enormous amounts of mechanical deformation while maintaining mechanical integrity and are also an essential set of geometries among chiral structures. This 3D helical structure can have broad potential applications in electromechanical devices such as nanoactuators, nanosensors and nanomotors. In contrast to the wrinkles reviewed in the previous section, mechanical buckling-induced self-assembled nanosprings can be obtained by removing the mechanical constraints in the out-of-plane direction and introducing a bilayer structure. Changes in these mechanical conditions enable the system not to be confined to 2D in-plane extended wrinkle deformation but to 3D deformation modes, such as rolling and twisting, leading to the formation of 3D rolled-up structures. This unique buckling behavior has been utilized in various studies to obtain 3D structures from 2D bilayers, coupled with the characteristic that nanomembranes typically exhibit anisotropic mechanical properties and deform alongside a particular direction. From an energy perspective, the helical shape usually results from the competition between bending and in-plane stretching energy driven by some internal or external force (including surface stress, residual stress, mismatch strain, and so on). The strain gradient in the flexible layer leads to bending along the direction with the smallest Young’s modulus[162,163] and the twisting of the bilayer structure can be achieved by the strain gradient field introduced by the mismatch strain between the anisotropic bilayers.
Many helical structures have been found in many inorganic thin film systems[164] and have recently been reported in ferroelectric oxides. Despite the fragile ionic or covalent bonds in oxides, Dong et al. fabricated self-assembled La0.7Sr0.3MnO3/BaTiO3 (LSMO/BTO) ferroelectric nanosprings with excellent elasticity and recovering capability via a water-peeling off process[66]. The BTO nanospring could be stretched or compressed to the geometric limit without breaking failure, thereby achieving a considerable scalability of 500% [Figure 8A and G]. The corresponding bilayer fabrication process with a strain gradient can produce high-quality spring structures of ferroelectric oxides, which have wide applicability. The phase-field simulations reveal that the excellent scalability originates from the continuously rotating ferroelastic domain structures, which provide displacement tolerance and energy to accommodate complex strains of mixed bending and twisting during mechanical deformation. Figure 8B and H show the strain component distribution εzz of nanosprings under compression and elongation, respectively. This unique strain state results in the transition of 180° strip domains distributed around the surface of the ferroelectric nanospring, as shown in Figure 8C and I. For example, during the compression/elongation process, the outer and inner surfaces of the nanospring are subjected to opposite strains, which results in different ferroelectric domain structures on the two surfaces [Figure 8D, E, J and K]. It is noteworthy that the bending moment is the largest in the region farthest laterally from the centerline of the 3D helix (i.e., the middle region of a single helical structure); therefore, the strain effect in this region is more evident. For example, when the nanospring is stretched, the compressive strain on the outer surface of the middle region is more evident than the tensile strain on the inner surface, so the electric dipoles in this region deflected perpendicular to the z-axis, forming a 180° domain structure in the out-of-plane of the BTO layer.
Figure 8. (A and G) In situ SEM images of the BTO nano-spring in compressive and tensile deformation, respectively. (B-F and H-L) Distribution of the strain component εzz, the domain structure, the outer surface domain, the inner surface domain, and the polarization component Pθ and strain distribution εθ along the middle line of the outer surface of the BTO nano-spring during compression and stretching, respectively. All panels reprinted with permission[66]. Copyright 2022, Wiley-VCH.
Figure 8F and L show the relationship between the polarization and the strain distribution on the outer surface of the BTO nanospring under compression and elongation, respectively. When the BTO thin films are twisted into the self-assembled nanosprings, the electromechanical coupling behavior differs from the direct relationship between polarization and strain in the previous ferroelectric film state [Figure 9]. Furthermore, the effect of shear strain is different in the two states. In the previous ferroelectric thin film state, the shear strain has almost no effect on the domain structure; however, when the BTO film is twisted into a nanospring state, the effect of shear strain cannot be ignored. Therefore, the nanospring design provides a novel conceptual framework and platform for the strain engineering of freestanding ferroelectric thin films. Regarding the 3D helical structure, many experimental and theoretical works[163,165-167] have reported the shape transition and regulation by external fields of the helical structure. Therefore, the helical structure of ferroelectric oxides can be further regulated in morphology and properties by changing the geometric parameters, modulus ratio and pre-strain of the bilayer film. For example, the mechanical deformation of the nanospring can also be regulated by applying an electron-beam-induced field, which is expected to be applied in flexible nanorobots.
Figure 9. (A and D) The polarization distribution of BTO freestanding thin films under compressive and tensile deformation, respectively. [(B and C) and (E and F)] The polarization-strain distribution on the centerline of BTO freestanding thin films during compression and elongation, respectively. All panels reprinted with permission[66]. Copyright 2022, Wiley-VCH.
Through the nonlinear mechanical model of Euler buckling, a series of novel functional mechanical structures can be realized, including other self-assembled superstructures (such as origami, kirigami and textile shapes), in addition to the previously reviewed wrinkled and helical structures. This mechanical modeling strategy based on these self-assembled 3D structure concepts can provide additional and unique ideas and solutions for developing and designing high-performance flexible ferroelectric devices. Furthermore, utilizing external stimuli (such as an external force or electric field) can qualitatively or even quantitatively manipulate the deformation of these mechanically buckling structures, providing a new approach for strain engineering and domain engineering of freestanding ferroelectric systems.
CONCLUSION AND OUTLOOK
As reviewed in this article, super-elastic ferroelectric materials are expected to be applied in a wide range of flexible electronic devices, including flexible memories, nanosensors, and nanogenerators. It is essential that ferroelectric materials maintain stable electrical performance under various mechanical deformations, such as stretching, compression, bending and twisting, which involves the dynamic behavior of mesoscopic domain structures in the ferroelectric materials. However, the direct observation of domain structure evolution during continuous deformation of freestanding ferroelectric thin films is challenging for current experimental methods. Moreover, phase-field simulations have become increasingly critical in revealing the super-elasticity of freestanding ferroelectric films and the dynamical behavior of domain structures in different nanostructures. Therefore, the combination of experimental observations and phase-field simulations plays a crucial role in expanding the research and application of super-elastic ferroelectric materials in the field of flexible electronics. To further play the guiding role of theoretical modeling in super-elastic freestanding ferroelectric thin films, the following crucial issues deserve attention and solutions:
Flexoelectric effect. The flexoelectric effect describes the coupling between the electric polarization and strain gradient. Since the strain gradient is inversely proportional to the spatial scale (i.e., the gradient of the strain concerning the spatial coordinate), the flexoelectric effect is size-dependent[168]. Therefore, the flexoelectric effect becomes increasingly evident and prominent as the size diminishes, and its contribution to the domain engineering of super-elastic freestanding ferroelectric thin films cannot be ignored. However, the theories and algorithms considering the flexoelectric effect in the phase-field model of super-elastic ferroelectrics still need further verification and improvement. For the freestanding ferroelectric system under mechanical deformation, it is necessary to establish a phase-field model considering the flexoelectric effect to study the origin, enhancement and application of the flexoelectric effect on super-elasticity.
Design, fabrication and regulation of novel and functional mechanical structures. In the regulation and application of freestanding ferroelectric systems, the design and preparation of novel and functional mechanical structures are also the focus of research. The influence of 3D superstructures (e.g., isometric helicoids, kagome shapes and hexagonal honeycombs) on the polarization distribution of ferroelectrics also requires systematic research and analysis.
Responsive behavior in multiple fields. Freestanding ferroelectric thin film systems exhibit several novel topological phenomena and it is essential to demonstrate the response and regulation of these topological structures in multi-physical fields (e.g., individual or mixed applications of mechanical, electric and magnetic fields). In contrast, the response behavior of super-elastic freestanding ferroelectric nanostructures under the external field still needs further research and analysis. For example, the stretching and compressing behavior of ferroelectric nano-springs may be modulated by an electron-beam-induced field, which could have potential applications in the design of flexible nanorobots.
DECLARATIONS
Authors’ contributionsConceived and designed the manuscript: Huang HB, Guo CQ
Drafted and revised the manuscript: Huang HB, Guo CQ
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work was financially supported by the National Natural Science Foundation of China (Grant No. 51972028) and the State Key Development Program for Basic Research of China (Grant No. 2019YFA0307900).
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2022.
REFERENCES
1. Hussain AM, Hussain MM. CMOS-technology-enabled flexible and stretchable electronics for internet of everything applications. Adv Mater 2016;28:4219-49.
2. Vilouras A, Heidari H, Gupta S, Dahiya R. Modeling of CMOS devices and circuits on flexible ultrathin chips. IEEE Trans Electron Devices 2017;64:2038-46.
3. Zhang H, Xiang L, Yang Y, et al. High-performance carbon nanotube complementary electronics and integrated sensor systems on ultrathin plastic foil. ACS Nano 2018;12:2773-9.
4. Comiskey B, Albert JD, Yoshizawa H, Jacobson J. An electrophoretic ink for all-printed reflective electronic displays. Nature 1998;394:253-5.
5. Rogers JA, Bao Z, Baldwin K, et al. Paper-like electronic displays: large-area rubber-stamped plastic sheets of electronics and microencapsulated electrophoretic inks. Proc Natl Acad Sci USA 2001;98:4835-40.
6. Gelinck GH, Huitema HE, van Veenendaal E, et al. Flexible active-matrix displays and shift registers based on solution-processed organic transistors. Nat Mater 2004;3:106-10.
7. McAlpine MC, Ahmad H, Wang D, Heath JR. Highly ordered nanowire arrays on plastic substrates for ultrasensitive flexible chemical sensors. Nat Mater 2007;6:379-84.
9. Lee HS, Chung J, Hwang G, et al. Flexible inorganic piezoelectric acoustic nanosensors for biomimetic artificial hair cells. Adv Funct Mater 2014;24:6914-21.
10. Yamamoto Y, Harada S, Yamamoto D, et al. Printed multifunctional flexible device with an integrated motion sensor for health care monitoring. Sci Adv 2016;2:e1601473.
11. Wang X, Liu Z, Zhang T. Flexible sensing electronics for wearable/attachable health monitoring. Small 2017;13:1602790.
12. Chen Y, Lu S, Zhang S, et al. Skin-like biosensor system via electrochemical channels for noninvasive blood glucose monitoring. Sci Adv 2017;3:e1701629.
13. Tee BC, Chortos A, Dunn RR, Schwartz G, Eason E, Bao Z. Tunable flexible pressure sensors using microstructured elastomer geometries for intuitive electronics. Adv Funct Mater 2014;24:5427-34.
14. Wang Y, Zhu C, Pfattner R, et al. A highly stretchable, transparent, and conductive polymer. Sci Adv 2017;3:e1602076.
15. Lu L, Ding W, Liu J, Yang B. Flexible PVDF based piezoelectric nanogenerators. Nano Energy 2020;78:105251.
16. Pan L, Yu G, Zhai D, et al. Hierarchical nanostructured conducting polymer hydrogel with high electrochemical activity. Proc Natl Acad Sci USA 2012;109:9287-92.
17. Sun JY, Zhao X, Illeperuma WR, et al. Highly stretchable and tough hydrogels. Nature 2012;489:133-6.
18. Kubo M, Li X, Kim C, et al. Stretchable microfluidic radiofrequency antennas. Adv Mater 2010;22:2749-52.
19. Gao Y, Ota H, Schaler EW, et al. Wearable microfluidic diaphragm pressure sensor for health and tactile touch monitoring. Adv Mater 2017;29:1701985.
20. Yan J, Ren CE, Maleski K, et al. Flexible MXene/graphene films for ultrafast supercapacitors with outstanding volumetric capacitance. Adv Funct Mater 2017;27:1701264.
21. Gao W, Zhu Y, Wang Y, Yuan G, Liu J. A review of flexible perovskite oxide ferroelectric films and their application. J Mater 2020;6:1-16.
22. Bertoldi K, Vitelli V, Christensen J, van Hecke M. Flexible mechanical metamaterials. Nat Rev Mater 2017;2:1-11.
23. Xue Z, Song H, Rogers JA, Zhang Y, Huang Y. Mechanically-guided structural designs in stretchable inorganic electronics. Adv Mater 2020;32:e1902254.
24. Kim DH, Ahn JH, Choi WM, et al. Stretchable and foldable silicon integrated circuits. Science 2008;320:507-11.
25. Bae HJ, Bae S, Yoon J, et al. Self-organization of maze-like structures via guided wrinkling. Sci Adv 2017;3:e1700071.
26. Peraza-hernandez EA, Hartl DJ, Malak Jr RJ, Lagoudas DC. Origami-inspired active structures: a synthesis and review. Smart Mater Struct 2014;23:094001.
28. Shyu TC, Damasceno PF, Dodd PM, et al. A kirigami approach to engineering elasticity in nanocomposites through patterned defects. Nat Mater 2015;14:785-9.
29. Callens SJ, Zadpoor AA. From flat sheets to curved geometries: origami and kirigami approaches. Materials Today 2018;21:241-64.
30. Meng Y, Zhao Y, Hu C, et al. All-graphene core-sheath microfibers for all-solid-state, stretchable fibriform supercapacitors and wearable electronic textiles. Adv Mater 2013;25:2326-31.
35. Sun H, Wang J, Wang Y, et al. Nonvolatile ferroelectric domain wall memory integrated on silicon. Nat Commun 2022;13:4332.
36. Muralt P. Ferroelectric thin films for micro-sensors and actuators: a review. J Micromecha Microeng 2000;10:136-46.
38. Kirby P, Komuro E, Imura M, Zhang Q, Su Q, Whatmore R. High frequency thin film ferroelectric acoustic resonators and filters. Integr Ferroelectr 2001;41:91-100.
39. Dragoman M, Aldrigo M, Modreanu M, Dragoman D. Extraordinary tunability of high-frequency devices using Hf0.3Zr0.7O2 ferroelectric at very low applied voltages. Appl Phys Lett 2017;110:103104.
40. Bowen CR, Kim HA, Weaver PM, Dunn S. Piezoelectric and ferroelectric materials and structures for energy harvesting applications. Energy Environ Sci 2014;7:25-44.
41. Zhang Y, Phuong PTT, Roake E, et al. Thermal energy harvesting using pyroelectric-electrochemical coupling in ferroelectric materials. Joule 2020;4:301-9.
42. Li Q, Han K, Gadinski MR, Zhang G, Wang Q. High energy and power density capacitors from solution-processed ternary ferroelectric polymer nanocomposites. Adv Mater 2014;26:6244-9.
43. Thakur VK, Gupta RK. Recent progress on ferroelectric polymer-based nanocomposites for high energy density capacitors: synthesis, dielectric properties, and future aspects. Chem Rev 2016;116:4260-317.
44. Xu K, Shi X, Dong S, Wang J, Huang H. Antiferroelectric phase diagram enhancing energy-storage performance by phase-field simulations. ACS Appl Mater Interfaces 2022;14:25770-80.
45. Xu S, Shi X, Pan H, et al. Strain engineering of energy storage performance in relaxor ferroelectric thin film capacitors. Adv Theory Simul 2022;5:2100324.
46. Ohigashi H, Koga K, Suzuki M, Nakanishi T, Kimura K, Hashimoto N. Piezoelectric and ferroelectric properties of P (VDF-TrFE) copolymers and their application to ultrasonic transducers. Ferroelectrics 1984;60:263-76.
47. Zhang S, Li F, Jiang X, Kim J, Luo J, Geng X. Advantages and challenges of relaxor-PbTiO3 Ferroelectric crystals for electroacoustic transducers-a review. Prog Mater Sci 2015;68:1-66.
48. Zhang G, Zhang X, Huang H, et al. Toward wearable cooling devices: highly flexible electrocaloric Ba0.67Sr0.33TiO3 nanowire arrays. Adv Mater 2016;28:4811-6.
49. Gao R, Shi X, Wang J, Zhang G, Huang H. Designed giant room-temperature electrocaloric effects in metal-free organic perovskite [MDABCO](NH4)I3 by phase-field simulations. Adv Funct Mater 2021;31:2104393.
50. Qian X, Han D, Zheng L, et al. High-entropy polymer produces a giant electrocaloric effect at low fields. Nature 2021;600:664-9.
51. Gao R, Shi X, Wang J, Huang H. Understanding electrocaloric cooling of ferroelectrics guided by phase-field modeling. J Am Ceram Soc 2022;105:3689-714.
52. Ge JF, Liu ZL, Liu C, et al. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO3. Nat Mater 2015;14:285-9.
53. Bégon-lours L, Rouco V, Sander A, et al. High-temperature-superconducting weak link defined by the ferroelectric field effect. Phys Rev Appl 2017:7.
54. Lynch CS, Chen L, Suo Z, Mcmeeking RM, Yang W. Crack growth in ferroelectric ceramics driven by cyclic polarization switching. J Intell Mater Syst Struct 1995;6:191-8.
55. Arias I, Serebrinsky S, Ortiz M. A phenomenological cohesive model of ferroelectric fatigue. Acta Mater 2006;54:975-84.
57. Bhansali US, Khan M, Alshareef H. Organic ferroelectric memory devices with inkjet-printed polymer electrodes on flexible substrates. Microelect Eng 2013;105:68-73.
58. Zabek D, Taylor J, Boulbar EL, Bowen CR. Micropatterning of flexible and free standing polyvinylidene difluoride (PVDF) films for enhanced pyroelectric energy transformation. Adv Energy Mater 2015;5:1401891.
59. Owczarek M, Hujsak KA, Ferris DP, et al. Flexible ferroelectric organic crystals. Nat Commun 2016;7:13108.
60. Guo M, Jiang J, Qian J, et al. Flexible robust and high-density FeRAM from array of organic ferroelectric nano-lamellae by self-assembly. Adv Sci 2019;6:1801931.
61. Dong G, Li S, Yao M, et al. Super-elastic ferroelectric single-crystal membrane with continuous electric dipole rotation. Science 2019;366:475-9.
62. Guo C, Dong G, Zhou Z, et al. Domain evolution in bended freestanding BaTiO3 ultrathin films: a phase-field simulation. Appl Phys Lett 2020;116:152903.
63. Dong G, Li S, Li T, et al. Periodic wrinkle-patterned single-crystalline ferroelectric oxide membranes with enhanced piezoelectricity. Adv Mater 2020;32:e2004477.
64. Zhou Y, Guo C, Dong G, et al. Tip-induced in-plane ferroelectric superstructure in zigzag-wrinkled BaTiO3 thin films. Nano Lett 2022;22:2859-66.
65. Guo M, Guo C, Han J, et al. Toroidal polar topology in strained ferroelectric polymer. Science 2021;371:1050-6.
66. Dong G, Hu Y, Guo C, et al. Self-assembled epitaxial ferroelectric oxide nanospring with super-scalability. Adv Mater 2022;34:e2108419.
67. Chen X, Li Q, Chen X, et al. Nano-imprinted ferroelectric polymer nanodot arrays for high density data storage. Adv Funct Mater 2013;23:3124-9.
68. Fujikake H, Sato H, Murashige T. Polymer-stabilized ferroelectric liquid crystal for flexible displays. Displays 2004;25:3-8.
69. Sekine T, Sugano R, Tashiro T, et al. Fully printed wearable vital sensor for human pulse rate monitoring using ferroelectric polymer. Sci Rep 2018;8:4442.
70. Han X, Chen X, Tang X, Chen Y, Liu J, Shen Q. Flexible polymer transducers for dynamic recognizing physiological signals. Adv Funct Mater 2016;26:3640-8.
71. Liu Z, Xu L, Zheng Q, et al. Human motion driven self-powered photodynamic system for long-term autonomous cancer therapy. ACS Nano 2020;14:8074-83.
72. Shi Q, Wang T, Lee C. MEMS based broadband piezoelectric ultrasonic energy harvester (PUEH) for enabling self-powered implantable biomedical devices. Sci Rep 2016;6:24946.
73. Ryu J, Priya S, Park C, et al. Enhanced domain contribution to ferroelectric properties in freestanding thick films. J Appl Phys 2009;106:024108.
74. Zuo Z, Chen B, Zhan Q, et al. Preparation and ferroelectric properties of freestanding Pb(Zr,Ti)O3 thin membranes. J Phys D Appl Phys 2012;45:185302.
75. Pesquera D, Parsonnet E, Qualls A, et al. Beyond substrates: strain engineering of ferroelectric membranes. Adv Mater 2020;32:e2003780.
76. Shi Q, Parsonnet E, Cheng X, et al. The role of lattice dynamics in ferroelectric switching. Nat Commun 2022;13:1110.
77. Tian M, Xu L, Yang Y. Perovskite oxide ferroelectric thin films. Adv Elect Mater 2022;8:2101409.
78. Jin C, Zhu Y, Han W, et al. Exchange bias in flexible freestanding La0.7Sr0.3MnO3/BiFeO3 membranes. Appl Phys Lett 2020;117:252902.
79. Xu R, Huang J, Barnard ES, et al. Strain-induced room-temperature ferroelectricity in SrTiO3 membranes. Nat Commun 2020;11:3141.
80. Chang L, You L, Wang J. The path to flexible ferroelectrics: approaches and progress. Jpn J Appl Phys 2018;57:0902A3.
81. Yao M, Cheng Y, Zhou Z, Liu M. Recent progress on the fabrication and applications of flexible ferroelectric devices. J Mater Chem C 2020;8:14-27.
82. Chiabrera FM, Yun S, Li Y, et al. Freestanding perovskite oxide films: synthesis, challenges, and properties. Annalen Physik 2022;534:2200084.
83. Li S, Wang Y, Yang M, et al. Ferroelectric thin films: performance modulation and application. Mater Adv 2022;3:5735-52.
84. Won SS, Seo H, Kawahara M, et al. Flexible vibrational energy harvesting devices using strain-engineered perovskite piezoelectric thin films. Nano Energy 2019;55:182-92.
85. De Dobbelaere C, Calzada ML, Jiménez R, et al. Aqueous solutions for low-temperature photoannealing of functional oxide films: reaching the 400 °C Si-technology integration barrier. J Am Chem Soc 2011;133:12922-5.
86. Bretos I, Jiménez R, Ricote J, Calzada ML. Low-temperature crystallization of solution-derived metal oxide thin films assisted by chemical processes. Chem Soc Rev 2018;47:291-308.
87. Bretos I, Jimenez R, Ricote J, Calzada ML. Low-temperature solution approaches for the potential integration of ferroelectric oxide films in flexible electronics. IEEE Trans Ultrason Ferroelectr Freq Control 2020;67:1967-79.
88. Bretos I, Jiménez R, Ricote J, Sirera R, Calzada ML. Photoferroelectric thin films for flexible systems by a three-in-one solution-based approach. Adv Funct Mater 2020;30:2001897.
89. Barrios Ó, Jiménez R, Ricote J, Tartaj P, Calzada ML, Bretos Í. A sustainable self-induced solution seeding approach for multipurpose BiFeO3 active layers in flexible electronic devices. Adv Funct Mater 2022;32:2112944.
90. Jiang J, Bitla Y, Huang CW, et al. Flexible ferroelectric element based on van der Waals heteroepitaxy. Sci Adv 2017;3:e1700121.
91. Zheng M, Li X, Ni H, Li X, Gao J. van der Waals epitaxy for highly tunable all-inorganic transparent flexible ferroelectric luminescent films. J Mater Chem C 2019;7:8310-5.
92. Bitla Y, Chu YH. van der Waals oxide heteroepitaxy for soft transparent electronics. Nanoscale 2020;12:18523-44.
93. Lee SA, Hwang JY, Kim ES, Kim SW, Choi WS. Highly oriented SrTiO3 Thin film on graphene substrate. ACS Appl Mater Inter 2017;9:3246-50.
94. Kum HS, Lee H, Kim S, et al. Heterogeneous integration of single-crystalline complex-oxide membranes. Nature 2020;578:75-81.
95. Wong WS, Sands T, Cheung NW. Damage-free separation of GaN thin films from sapphire substrates. Appl Phys Lett 1998;72:599-601.
96. Xu J, Zhang R, Wang Y, et al. Preparation of large area freestanding GaN by laser lift-off technology. Mater Lett 2002;56:43-6.
97. Lin I, Hsieh K, Lee K, Tai N. Preparation of ferroelectric Pb(Zr1-xTix)O3/Si films by laser lift-off technique. J Eur Ceram Soc 2004;24:975-8.
98. Lee CH, Kim SJ, Oh Y, Kim MY, Yoon Y, Lee H. Use of laser lift-off for flexible device applications. J Appl Phys 2010;108:102814.
99. Zhang Y, Ma C, Lu X, Liu M. Recent progress on flexible inorganic single-crystalline functional oxide films for advanced electronics. Mater Horiz 2019;6:911-30.
100. Bakaul SR, Serrao CR, Lee M, et al. Single crystal functional oxides on silicon. Nat Commun 2016;7:10547.
101. Bakaul SR, Prokhorenko S, Zhang Q, et al. Freestanding ferroelectric bubble domains. Adv Mater 2021;33:e2105432.
102. Lu D, Baek DJ, Hong SS, Kourkoutis LF, Hikita Y, Hwang HY. Synthesis of freestanding single-crystal perovskite films and heterostructures by etching of sacrificial water-soluble layers. Nat Mater 2016;15:1255-60.
103. Baek DJ, Lu D, Hikita Y, Hwang HY, Kourkoutis LF. Ultrathin epitaxial barrier layer to avoid thermally induced phase transformation in oxide heterostructures. ACS Appl Mater Inter 2017;9:54-9.
104. Hong SS, Yu JH, Lu D, et al. Two-dimensional limit of crystalline order in perovskite membrane films. Sci Adv 2017;3:eaao5173.
105. Ji D, Cai S, Paudel TR, et al. Freestanding crystalline oxide perovskites down to the monolayer limit. Nature 2019;570:87-90.
106. Han L, Fang Y, Zhao Y, et al. Giant uniaxial strain ferroelectric domain tuning in freestanding PbTiO3 films. Adv Mater Inter 2020;7:1901604.
107. Takahashi R, Lippmaa M. Sacrificial water-soluble BaO layer for fabricating free-standing piezoelectric membranes. ACS Appl Mater Inter 2020;12:25042-9.
108. Zhong H, Li M, Zhang Q, et al. Large-scale Hf0.5Zr0.5O2 membranes with robust ferroelectricity. Adv Mater 2022;34:e2109889.
109. Guo R, You L, Lin W, et al. Continuously controllable photoconductance in freestanding BiFeO3 by the macroscopic flexoelectric effect. Nat Commun 2020;11:2571.
110. Peng B, Peng RC, Zhang YQ, et al. Phase transition enhanced superior elasticity in freestanding single-crystalline multiferroic BiFeO3 membranes. Sci Adv 2020;6:eaba5847.
111. Jin C, Zhu Y, Li X, et al. Super-flexible freestanding BiMnO3 membranes with stable ferroelectricity and ferromagnetism. Adv Sci 2021;8:e2102178.
112. Han L, Addiego C, Prokhorenko S, et al. High-density switchable skyrmion-like polar nanodomains integrated on silicon. Nature 2022;603:63-7.
113. Elangovan H, Barzilay M, Seremi S, et al. Giant superelastic piezoelectricity in flexible ferroelectric BaTiO3 membranes. ACS Nano 2020;14:5053-60.
114. Cai S, Lun Y, Ji D, et al. Enhanced polarization and abnormal flexural deformation in bent freestanding perovskite oxides. Nat Commun 2022;13:5116.
116. Artyukhin S, Delaney KT, Spaldin NA, Mostovoy M. Landau theory of topological defects in multiferroic hexagonal manganites. Nat Mater 2014;13:42-9.
117. Xue F, Wang X, Shi Y, Cheong S, Chen L. Strain-induced incommensurate phases in hexagonal manganites. Phys Rev B 2017;96:104109.
118. Wang J, Shi S, Chen L, Li Y, Zhang T. Phase-field simulations of ferroelectric/ferroelastic polarization switching. Acta Materialia 2004;52:749-64.
119. Cao W. Constructing landau-ginzburg-devonshire type models for ferroelectric systems based on symmetry. Ferroelectrics 2008;375:28-39.
120. Chen L. Phase-field method of phase transitions/domain structures in ferroelectric thin films: a review. J Am Ceram Soc 2008;91:1835-44.
121. Chen HT, Soh AK, Ni Y. Phase field modeling of flexoelectric effects in ferroelectric epitaxial thin films. Acta Mech 2014;225:1323-33.
122. Wang J, Wang B, Chen L. Understanding, predicting, and designing ferroelectric domain structures and switching guided by the phase-field method. Annu Rev Mater Res 2019;49:127-52.
123. Peng R, Cheng X, Peng B, Zhou Z, Chen L, Liu M. Domain patterns and super-elasticity of freestanding BiFeO3 membranes via phase-field simulations. Acta Materialia 2021;208:116689.
124. Peng R, Cheng X, Peng B, Zhou Z, Chen L, Liu M. Boundary conditions manipulation of polar vortex domains in BiFeO3 membranes via phase-field simulations. J Phys D Appl Phys 2021;54:495301.
125. Chen WJ, Zheng Y, Xiong WM, Feng X, Wang B, Wang Y. Effect of mechanical loads on stability of nanodomains in ferroelectric ultrathin films: towards flexible erasing of the non-volatile memories. Sci Rep 2014;4:5339.
126. Lacour S, Jones J, Suo Z, Wagner S. Design and performance of thin metal film interconnects for skin-like electronic circuits. IEEE Electron Device Lett 2004;25:179-81.
127. Cheng H, Zhang Y, Hwang K, Rogers JA, Huang Y. Buckling of a stiff thin film on a pre-strained bi-layer substrate. Int J Solids Struct 2014;51:3113-8.
128. Pan K, Ni Y, He L, Huang R. Nonlinear analysis of compressed elastic thin films on elastic substrates: from wrinkling to buckle-delamination. Int J Solids Struct 2014;51:3715-26.
129. Xu F, Potier-ferry M, Belouettar S, Cong Y. 3D finite element modeling for instabilities in thin films on soft substrates. Int J Solids Struct 2014;51:3619-32.
130. Yan D, Zhang K, Hu G. Wrinkling of structured thin films via contrasted materials. Soft Matter 2016;12:3937-42.
131. Park HG, Jeong HC, Jung YH, Seo DS. Control of the wrinkle structure on surface-reformed poly(dimethylsiloxane) via ion-beam bombardment. Sci Rep 2015;5:12356.
132. Zhu W, Low T, Perebeinos V, et al. Structure and electronic transport in graphene wrinkles. Nano Lett 2012;12:3431-6.
133. Chung JY, Nolte AJ, Stafford CM. Diffusion-controlled, self-organized growth of symmetric wrinkling patterns. Adv Mater 2009;21:1358-62.
134. Guvendiren M, Yang S, Burdick JA. Swelling-induced surface patterns in hydrogels with gradient crosslinking density. Adv Funct Mater 2009;19:3038-45.
135. Jiang H, Khang DY, Song J, Sun Y, Huang Y, Rogers JA. Finite deformation mechanics in buckled thin films on compliant supports. Proc Natl Acad Sci USA 2007;104:15607-12.
137. Huang Z, Hong W, Suo Z. Nonlinear analyses of wrinkles in a film bonded to a compliant substrate. J Mech Phys Solids 2005;53:2101-18.
138. Genzer J, Groenewold J. Soft matter with hard skin: From skin wrinkles to templating and material characterization. Soft Matter 2006;2:310-23.
139. Audoly B, Boudaoud A. Buckling of a stiff film bound to a compliant substrate-part I: formulation, linear stability of cylindrical patterns, secondary bifurcations. J Mech Phys Solids 2008;56:2401-21.
140. Zhang Y, Zhang F, Yan Z, et al. Printing, folding and assembly methods for forming 3D mesostructures in advanced materials. Nat Rev Mater 2017:2.
141. Rogers JA, Someya T, Huang Y. Materials and mechanics for stretchable electronics. Science 2010;327:1603-7.
142. Kim JB, Kim P, Pégard NC, et al. Wrinkles and deep folds as photonic structures in photovoltaics. Nat Photon 2012;6:327-32.
143. Zhang W, Zhang Y, Qiu J, Zhao Z, Liu N. Topological structures of transition metal dichalcogenides: a review on fabrication, effects, applications, and potential. InfoMat 2021;3:133-54.
144. Stafford CM, Harrison C, Beers KL, et al. A buckling-based metrology for measuring the elastic moduli of polymeric thin films. Nat Mater 2004;3:545-50.
145. Chung JY, Nolte AJ, Stafford CM. Surface wrinkling: a versatile platform for measuring thin-film properties. Adv Mater 2011;23:349-68.
146. Dervaux J, Couder Y, Guedeau-Boudeville MA, Ben Amar M. Shape transition in artificial tumors: from smooth buckles to singular creases. Phys Rev Lett 2011;107:018103.
147. Guvendiren M, Burdick JA, Yang S. Solvent induced transition from wrinkles to creases in thin film gels with depth-wise crosslinking gradients. Soft Matter 2010;6:5795.
148. Tan Y, Hu B, Song J, Chu Z, Wu W. Bioinspired multiscale wrinkling patterns on curved substrates: an overview. Nanomicro Lett 2020;12:101.
149. Naumov II, Bellaiche L, Fu H. Unusual phase transitions in ferroelectric nanodisks and nanorods. Nature 2004;432:737-40.
150. Tang YL, Zhu YL, Ma XL, et al. Observation of a periodic array of flux-closure quadrants in strained ferroelectric PbTiO3 films. Science 2015;348:547-51.
151. Hadjimichael M, Li Y, Zatterin E, et al. Metal-ferroelectric supercrystals with periodically curved metallic layers. Nat Mater 2021;20:495-502.
152. Yadav AK, Nelson CT, Hsu SL, et al. Observation of polar vortices in oxide superlattices. Nature 2016;530:198-201.
153. Hong Z, Damodaran AR, Xue F, et al. Stability of polar vortex lattice in ferroelectric superlattices. Nano Lett 2017;17:2246-52.
154. Liu D, Shi X, Wang J, Cheng X, Huang H. Phase-field simulations of surface charge-induced ferroelectric vortex. J Phys D Appl Phys 2021;54:405302.
155. Liu D, Wang J, Jafri HM, et al. Phase-field simulations of vortex chirality manipulation in ferroelectric thin films. NPJ Quantum Mater 2022:7.
156. Das S, Tang YL, Hong Z, et al. Observation of room-temperature polar skyrmions. Nature 2019;568:368-72.
157. Zhang Y, Li Q, Huang H, Hong J, Wang X. Strain manipulation of ferroelectric skyrmion bubbles in a freestanding PbTiO3 film: a phase field simulation. Phys Rev B 2022:105.
158. Wang YJ, Feng YP, Zhu YL, et al. Polar meron lattice in strained oxide ferroelectrics. Nat Mater 2020;19:881-6.
159. Vasudevan RK, Chen YC, Tai HH, et al. Exploring topological defects in epitaxial BiFeO3 thin films. ACS Nano 2011;5:879-87.
160. Wang X, Mostovoy M, Han MG, et al. Unfolding of vortices into topological stripes in a multiferroic material. Phys Rev Lett 2014;112:247601.
161. Shimada T, Lich le V, Nagano K, Wang J, Kitamura T. Hierarchical ferroelectric and ferrotoroidic polarizations coexistent in nano-metamaterials. Sci Rep 2015;5:14653.
162. Cavallo F, Lagally MG. Semiconductors turn soft: inorganic nanomembranes. Soft Matter 2010;6:439-55.
163. Chen Z, Huang G, Trase I, Han X, Mei Y. Mechanical self-assembly of a strain-engineered flexible layer: wrinkling, rolling, and twisting. Phys Rev Applied 2016:5.
165. Guo Q, Mehta AK, Grover MA, Chen W, Lynn DG, Chen Z. Shape selection and multi-stability in helical ribbons. Appl Phys Lett 2014;104:211901.
166. Guo Q, Chen Z, Li W, et al. Mechanics of tunable helices and geometric frustration in biomimetic seashells. EPL Europhys Lett 2014;105:64005.
167. Yu X, Zhang L, Hu N, et al. Shape formation of helical ribbons induced by material anisotropy. Appl Phys Lett 2017;110:091901.
Cite This Article
How to Cite
Guo, C.; Huang, H. Design of super-elastic freestanding ferroelectric thin films guided by phase-field simulations. Microstructures. 2022, 2, 2022021. http://dx.doi.org/10.20517/microstructures.2022.20
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.

































Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.